
Cunningham project
Encyclopedia
The Cunningham project aims to find factor
s of large numbers of the form
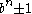
for b = 2, 3, 5, 6, 7, 10, 11, 12 and large exponents n. The project is named after Allan Joseph Champneys Cunningham
, who published the first version of the table together with Herbert J. Woodall
in 1925. Sometimes it is referred to as one of the oldest continuously ongoing activities in computational number theory
.
A recently published version of the tables can be found in "Factorizations of bn ± 1, b = 2, 3, 5, 6, 7, 10, 11, 12 up to high powers" by John Brillhart
, Derrick Henry Lehmer
, John L. Selfridge, Bryant Tuckerman, & Samuel S. Wagstaff Jr.
, AMS (2002). The most recent version of the tables can be found at the Cunningham Project website.
The Brent-Montgomery-te Riele table forms an extension to the Cunningham tables, for 12 < b < 1000.
Current limits of the exponents of the Cunningham tables are:
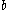 and
and  .
.

for any value of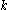 , and
, and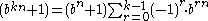
when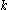 is odd.
is odd.
Also that, .
.
Thus, it turns out that both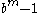 and
and 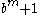 are factors of
are factors of  , if
, if 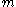 divides
divides  and
and 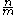 is even. Only
is even. Only  is a factor of
is a factor of 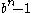 , if
, if 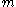 divides
divides  and
and 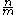 is odd. Also,
is odd. Also, 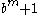 is a factor of
is a factor of 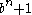 , if
, if 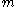 divides
divides  and
and 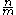 is odd.
is odd.
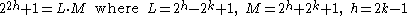
This factorization was discovered for one value (n = 14) by Aurifeuille and the general form was subsequently given by Lucas. Here are the Aurifeuillian factorizations for the other bases.
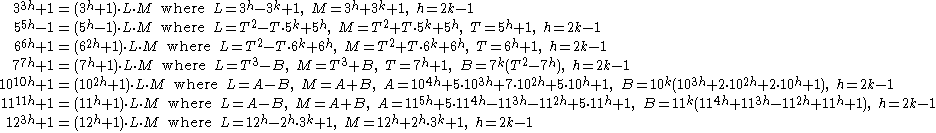
So, there exist an Aurifeuillian factorization for base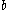 for any exponent of the form
for any exponent of the form 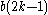 for integral values of
for integral values of 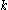 . Note that the Aurifeuillian factorization of base 5 is on the negative side, while for the other bases 2, 3, 6, 7, 10, 11, 12 it is on the positive side.
. Note that the Aurifeuillian factorization of base 5 is on the negative side, while for the other bases 2, 3, 6, 7, 10, 11, 12 it is on the positive side.
 will always be of the form
will always be of the form 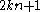 . When the exponent
. When the exponent  is prime, algebraic and Aurifeuillian factors are not possible, except for the trivial factor of
is prime, algebraic and Aurifeuillian factors are not possible, except for the trivial factor of  for
for 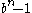 and
and 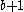 for
for 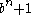 .
.
For Mersenne numbers of the form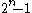 , even this trivial factor is not possible for prime values of
, even this trivial factor is not possible for prime values of  , so any factor of it should be of the form
, so any factor of it should be of the form  . In general, any factor of
. In general, any factor of 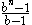 is of the form
is of the form 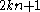 ,
,  and
and  is prime, except when
is prime, except when  is a factor of
is a factor of  . In such cases,
. In such cases, 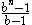 is divisible by
is divisible by  itself.
itself.
Cunningham numbers of the form can only be prime if
can only be prime if 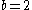 and
and  is prime, assuming that
is prime, assuming that 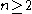 , and numbers of the form
, and numbers of the form 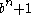 can only be prime if
can only be prime if 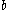 is even and
is even and  is a power of 2, considering the fact that
is a power of 2, considering the fact that 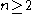 again. Numbers of the form
again. Numbers of the form  are known as Generalized Fermat Numbers, which when
are known as Generalized Fermat Numbers, which when  , are known as Fermat Numbers. In general, any factor of the Fermat Number
, are known as Fermat Numbers. In general, any factor of the Fermat Number  is of the form
is of the form 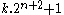 .
.
Only the first five Fermat numbers, k = 0, 1, 2, 3, 4 corresponding to 3, 5, 17, 257 and 65537 are known to be prime. All Fermat numbers from k = 5 to k = 32 are known to be composite. Fermat numbers till k = 11 are fully factorized.
Does there exist any squares of primes that divide Mersenne numbers of the form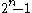 , for prime values of
, for prime values of  ? If such a prime exists, it must be a Wieferich prime, satisfying
? If such a prime exists, it must be a Wieferich prime, satisfying  . Only two such primes are known 1093 and 3511, out of a very deep search, and neither of these square divide a Mersenne number at all, for any prime value of
. Only two such primes are known 1093 and 3511, out of a very deep search, and neither of these square divide a Mersenne number at all, for any prime value of  .
.
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
s of large numbers of the form
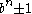
for b = 2, 3, 5, 6, 7, 10, 11, 12 and large exponents n. The project is named after Allan Joseph Champneys Cunningham
Allan Joseph Champneys Cunningham
The British mathematician Allan Joseph Champneys Cunningham started a military career with the East India Company's Bengal Engineers. During 1871–1881, he was Instructor in Mathematics at the Thomason Civil Engineering College, Roorkee...
, who published the first version of the table together with Herbert J. Woodall
H. J. Woodall
Herbert J. Woodall was a British mathematician.In 1925 Lt.-Col. Allan J.C. Cunningham and Woodall gathered together all that was known about the primality and factorization of such numbers and published a small book of tables...
in 1925. Sometimes it is referred to as one of the oldest continuously ongoing activities in computational number theory
Computational number theory
In mathematics, computational number theory, also known as algorithmic number theory, is the study of algorithms for performing number theoretic computations...
.
A recently published version of the tables can be found in "Factorizations of bn ± 1, b = 2, 3, 5, 6, 7, 10, 11, 12 up to high powers" by John Brillhart
John Brillhart
John David Brillhart is a mathematician, professor emeritus at the University of Arizona. He is known for his work in integer factorization, including the development of the continued fraction factorization method. He has been a principal participant in the Cunningham project.Brillhart received his...
, Derrick Henry Lehmer
Derrick Henry Lehmer
Derrick Henry "Dick" Lehmer was an American mathematician who refined Édouard Lucas' work in the 1930s and devised the Lucas–Lehmer test for Mersenne primes...
, John L. Selfridge, Bryant Tuckerman, & Samuel S. Wagstaff Jr.
Samuel S. Wagstaff Jr.
Samuel Standfield Wagstaff, Jr. is an American mathematician and computer scientist whose research interests are in the areas of cryptography, parallel computation, and analysis of algorithms, especially number theoretic algorithms...
, AMS (2002). The most recent version of the tables can be found at the Cunningham Project website.
The Brent-Montgomery-te Riele table forms an extension to the Cunningham tables, for 12 < b < 1000.
Current limits of the exponents of the Cunningham tables are:
| Base | 2 | 3 | 5 | 6 | 7 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|
| Limit | 1200 | 600 | 450 | 400 | 400 | 400 | 300 | 300 |
Properties of Cunningham Factors
In the Cunningham tables, we eliminate two types of factors before factoring the remaining cofactor. The first type is Algebraic Factors, which are derived from a lower exponent. The second type is Aurifeuillian Factors, in which the whole number can be split into two parts directly, for certain combination of values of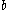 and
and  .
.Algebraic Factorizations
It is trivial from elementary algebra that
for any value of
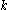 , and
, and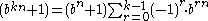
when
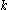 is odd.
is odd.Also that,
 .
.Thus, it turns out that both
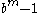 and
and 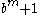 are factors of
are factors of  , if
, if 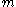 divides
divides  and
and 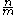 is even. Only
is even. Only  is a factor of
is a factor of 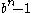 , if
, if 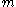 divides
divides  and
and 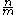 is odd. Also,
is odd. Also, 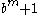 is a factor of
is a factor of 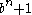 , if
, if 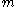 divides
divides  and
and 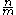 is odd.
is odd.Aurifeuillian Factorizations
Consider the identity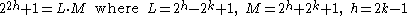
This factorization was discovered for one value (n = 14) by Aurifeuille and the general form was subsequently given by Lucas. Here are the Aurifeuillian factorizations for the other bases.
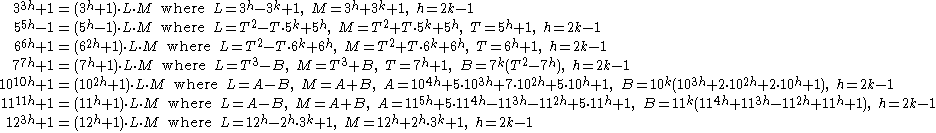
So, there exist an Aurifeuillian factorization for base
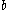 for any exponent of the form
for any exponent of the form 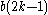 for integral values of
for integral values of 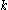 . Note that the Aurifeuillian factorization of base 5 is on the negative side, while for the other bases 2, 3, 6, 7, 10, 11, 12 it is on the positive side.
. Note that the Aurifeuillian factorization of base 5 is on the negative side, while for the other bases 2, 3, 6, 7, 10, 11, 12 it is on the positive side.Other factors
Once the algebraic and Aurifeuillian factors are removed, the other factors of will always be of the form
will always be of the form 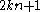 . When the exponent
. When the exponent  is prime, algebraic and Aurifeuillian factors are not possible, except for the trivial factor of
is prime, algebraic and Aurifeuillian factors are not possible, except for the trivial factor of  for
for 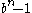 and
and 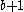 for
for 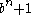 .
.For Mersenne numbers of the form
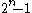 , even this trivial factor is not possible for prime values of
, even this trivial factor is not possible for prime values of  , so any factor of it should be of the form
, so any factor of it should be of the form  . In general, any factor of
. In general, any factor of 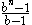 is of the form
is of the form 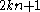 ,
,  and
and  is prime, except when
is prime, except when  is a factor of
is a factor of  . In such cases,
. In such cases, 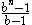 is divisible by
is divisible by  itself.
itself.Cunningham numbers of the form
 can only be prime if
can only be prime if 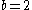 and
and  is prime, assuming that
is prime, assuming that 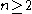 , and numbers of the form
, and numbers of the form 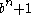 can only be prime if
can only be prime if 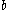 is even and
is even and  is a power of 2, considering the fact that
is a power of 2, considering the fact that 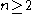 again. Numbers of the form
again. Numbers of the form  are known as Generalized Fermat Numbers, which when
are known as Generalized Fermat Numbers, which when  , are known as Fermat Numbers. In general, any factor of the Fermat Number
, are known as Fermat Numbers. In general, any factor of the Fermat Number  is of the form
is of the form 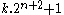 .
.Only the first five Fermat numbers, k = 0, 1, 2, 3, 4 corresponding to 3, 5, 17, 257 and 65537 are known to be prime. All Fermat numbers from k = 5 to k = 32 are known to be composite. Fermat numbers till k = 11 are fully factorized.
Does there exist any squares of primes that divide Mersenne numbers of the form
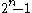 , for prime values of
, for prime values of  ? If such a prime exists, it must be a Wieferich prime, satisfying
? If such a prime exists, it must be a Wieferich prime, satisfying  . Only two such primes are known 1093 and 3511, out of a very deep search, and neither of these square divide a Mersenne number at all, for any prime value of
. Only two such primes are known 1093 and 3511, out of a very deep search, and neither of these square divide a Mersenne number at all, for any prime value of  .
.
