Reinhardt domain
Encyclopedia
In mathematics, especially several complex variables
, an open subset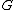
of Cn is called Reinhardt domain if 
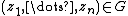implies 
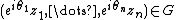for all real numbers 
.
The reason for studying these kinds of domains is that logarithmically convex Reinhardt domain are the domains of convergence of power series in several complex variables. Note that in one complex variable, a logarithmically convex Reinhardt domain is simply a disc
.
The intersection of logarithmically convex Reinhardt domains is still a logarithmically convex Reinhardt domain, so for every Reinhardt domain, there is a smallest logarithmically convex Reinhardt domain which contains it.
A simple example of logarithmically convex Reinhardt domains is a polydisc, that is, a product of disks.
Thullen's classical result says that a 2-dimensional bounded Reinhard domain containing the origin is biholomorphic to one of the following domains provided that the orbit of the origin by the automophism group has positive dimension:
(1)
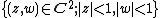(polydisc);
(2)
(unit ball);
(3)
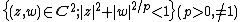(Thullen domain).
In 1978, Toshikazu Sunada
established a generalization of Thullen's result, and proved that two
-dimensional bounded Reinhardt domains 
and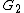 
are mutually biholomorphic if and only if there exists a transformation 
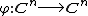given by
, 
being a
permutation of the indices), such that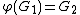
.
Several complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
, an open subset
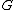of Cn is called Reinhardt domain if 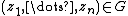implies 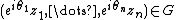for all real numbers .The reason for studying these kinds of domains is that logarithmically convex Reinhardt domain are the domains of convergence of power series in several complex variables. Note that in one complex variable, a logarithmically convex Reinhardt domain is simply a disc
Disk (mathematics)
In geometry, a disk is the region in a plane bounded by a circle.A disk is said to be closed or open according to whether or not it contains the circle that constitutes its boundary...
.
The intersection of logarithmically convex Reinhardt domains is still a logarithmically convex Reinhardt domain, so for every Reinhardt domain, there is a smallest logarithmically convex Reinhardt domain which contains it.
A simple example of logarithmically convex Reinhardt domains is a polydisc, that is, a product of disks.
Thullen's classical result says that a 2-dimensional bounded Reinhard domain containing the origin is biholomorphic to one of the following domains provided that the orbit of the origin by the automophism group has positive dimension:
(1)
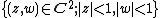(polydisc);(2)
(unit ball);(3)
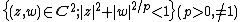(Thullen domain).In 1978, Toshikazu Sunada
Toshikazu Sunada
is a Japanese mathematician and author of many books and essays on mathematics and mathematical sciences. He is professor of mathematics at Meiji University, Tokyo, and is also professor emeritus of Tohoku University, Tohoku, Japan...
established a generalization of Thullen's result, and proved that two
-dimensional bounded Reinhardt domains and 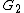are mutually biholomorphic if and only if there exists a transformation 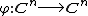given by, being apermutation of the indices), such that
.
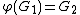