Reduced dynamics
Encyclopedia
In quantum mechanics
, especially in the study of open quantum system
s, reduced dynamics refers to the time evolution
of a density matrix
for a system coupled to an environment. Consider a system and environment initially in the state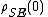
(which in general may be entangled
) and undergoing unitary evolution given by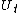
. Then the reduced dynamics of the system alone is simply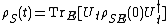
If we assume that the mapping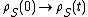
is linear and completely positive, then the reduced dynamics can be represented by a quantum operation
. This mean we can express it in the operator-sum form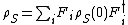
where the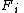
are operators on the Hilbert space
of the system alone, and no reference is made to the environment. In particular, if the system and environment are initially in a product state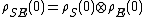
, it can be shown that the reduced dynamics are completely positive. However, the most general possible reduced dynamics are not completely positive.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, especially in the study of open quantum system
Open quantum system
In physics, an open quantum system is a quantum system which is found to be in interaction with an external quantum system, the environment...
s, reduced dynamics refers to the time evolution
Time evolution
Time evolution is the change of state brought about by the passage of time, applicable to systems with internal state . In this formulation, time is not required to be a continuous parameter, but may be discrete or even finite. In classical physics, time evolution of a collection of rigid bodies...
of a density matrix
Density matrix
In quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
for a system coupled to an environment. Consider a system and environment initially in the state
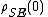(which in general may be entangledQuantum entanglement
Quantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
) and undergoing unitary evolution given by
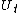. Then the reduced dynamics of the system alone is simply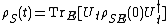If we assume that the mapping
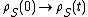is linear and completely positive, then the reduced dynamics can be represented by a quantum operationQuantum operation
In quantum mechanics, a quantum operation is a mathematical formalism used to describe a broad class of transformations that a quantum mechanical system can undergo. This was first discussed as a general stochastic transformation for a density matrix by George Sudarshan...
. This mean we can express it in the operator-sum form
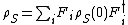
where the
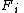are operators on the Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
of the system alone, and no reference is made to the environment. In particular, if the system and environment are initially in a product state
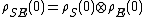, it can be shown that the reduced dynamics are completely positive. However, the most general possible reduced dynamics are not completely positive.