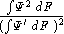Redescending M-estimator
Encyclopedia
In statistics
, Redescending M-estimators are Ψ-type M-estimator
s which have Ψ functions that are non-decreasing near the origin, but decreasing toward 0 far from the origin. Their ψ functions can be chosen to redescend smoothly to zero, so that they usually satisfy Ψ(x) = 0 for all x with |x| > r, where r is referred to as the minimum rejected point.
Due to these properties of the ψ function, these kinds of estimators are very efficient, have a high breakdown point and, unlike other outlier rejection techniques, they do not suffer from a masking effect. They are efficient because they completely reject gross outliers, and do not completely ignore moderately large outliers (like median).
The redescending M-estimators are slightly more efficient than the Huber estimator
for several symmetric, wider tailed distributions, but about 20% more efficient than the Huber estimator for the Cauchy distribution
. This is because they completely reject gross outliers, while the Huber estimator effectively treats these the same as moderate outliers.
Unlike other outlier rejection techniques, they do not suffer from masking effects.
where F is the mixture model distribution.
This effect is particularly harmful when a large negative values of ψ'(x) combines with a large positive values of ψ2(x), and there is a cluster of outliers near x.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, Redescending M-estimators are Ψ-type M-estimator
M-estimator
In statistics, M-estimators are a broad class of estimators, which are obtained as the minima of sums of functions of the data. Least-squares estimators and many maximum-likelihood estimators are M-estimators. The definition of M-estimators was motivated by robust statistics, which contributed new...
s which have Ψ functions that are non-decreasing near the origin, but decreasing toward 0 far from the origin. Their ψ functions can be chosen to redescend smoothly to zero, so that they usually satisfy Ψ(x) = 0 for all x with |x| > r, where r is referred to as the minimum rejected point.
Due to these properties of the ψ function, these kinds of estimators are very efficient, have a high breakdown point and, unlike other outlier rejection techniques, they do not suffer from a masking effect. They are efficient because they completely reject gross outliers, and do not completely ignore moderately large outliers (like median).
Advantages
Redescending M-estimators have very low breakdown points (close to 0.5), and their Ψ function can be chosen to redescend smoothly to 0. This means that moderately large outliers are not ignored completely, and greatly improves the efficiency of the redescending M-estimator.The redescending M-estimators are slightly more efficient than the Huber estimator
Huber Loss Function
In statistical theory, the Huber loss function is a function used in robust estimation that allows construction of an estimate which allows the effect of outliers to be reduced, while treating non-outliers in a more standard way.-Definition:...
for several symmetric, wider tailed distributions, but about 20% more efficient than the Huber estimator for the Cauchy distribution
Cauchy distribution
The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
. This is because they completely reject gross outliers, while the Huber estimator effectively treats these the same as moderate outliers.
Unlike other outlier rejection techniques, they do not suffer from masking effects.
Disadvantages
The M-estimating equation for a redescending estimator may not have a unique solution.Choosing redescending Ψ functions
When choosing a redescending Ψ functions, we must take care that it does not descend too steeply, which may have a very bad influence on the denominator in the expression for the asymptotic variancewhere F is the mixture model distribution.
This effect is particularly harmful when a large negative values of ψ'(x) combines with a large positive values of ψ2(x), and there is a cluster of outliers near x.
Examples
1. Hampel's three-part M estimators have Ψ functions which are odd functions and defined for any x by:-

This function is plotted in the following figure for a=1.645, b=3 and r=6.5.

2. Tukey's biweight or bisquare M estimators have Ψ functions for any positive k, which defined by:
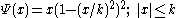
This function is plotted in the following figure for k=5.

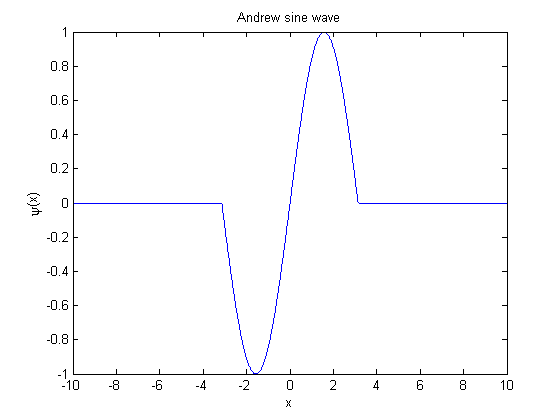
3. Andrew's sine wave M estimator has the following Ψ function:
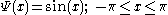
This function is plotted in the following figure.