
Reciprocity in network
Encyclopedia
Theoretical efforts have been made to study the nontrivial properties of complex networks, such as clustering
, scale-free
degree distribution
, community structures, etc. Here Reciprocity is another quantity to specifically characterize directed networks
. Link reciprocity measures the tendency of vertex pairs to form mutual connections between each other.
of occurring double links (with opposite directions) between vertice pairs. This problem is fundamental for several
reasons. First, in the networks that transport information or material (such as email networks
, World Wide Web (WWW) , World Trade Web , or Wikipedia itself ), the mutual links will facilitate the transportation process. Second, when analyzing directed networks, people often treat them as undirected ones for simplicity; therefore the information obtained from reciprocity studies tells us how much is deviated from the truth when a directed network is treated as undirected (for example, when measuring the cluster coefficient). Finally, detecting
nontrivial patterns of reciprocity is interesting, since it can reveal possible mechanisms and organizing principles that shape the observed network topology.
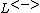 to the total number of links L
to the total number of links L
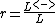
With this definition,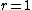 is for a purely bidirectional network while
is for a purely bidirectional network while
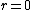 for a purely unidirectional one. Real networks have an intermediate value between 0 and 1.
for a purely unidirectional one. Real networks have an intermediate value between 0 and 1.
However, this definition of reciprocity has some defects. It cannot tell the relative difference of reciprocity compared with purely random network with the same number of vertices and edges. The useful information from reciprocity is not the value itself, but whether mutual links occur more or less often than expected by chance. Besides, in those networks containing self-linking loops (links starting and ending at the same vertex), the self-linking loops should be excluded when calculating L.
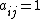 if a link from i to j is there, and
if a link from i to j is there, and 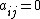 if not):
if not):
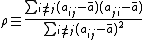 ,
,
where the average value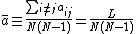 .
.
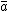 measures the ratio of observed to possible directed links (link density), and self-linking loops are now excluded from L because of i not equal to j.
measures the ratio of observed to possible directed links (link density), and self-linking loops are now excluded from L because of i not equal to j.
The definition can be written in the following simple form:

The new definition of reciprocity gives an absolute quantity which directly allows one to distinguish between reciprocal (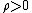 ) and antireciprocal (
) and antireciprocal (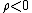 ) networks, with mutual links occurring more and less often than random respectively.
) networks, with mutual links occurring more and less often than random respectively.
If all the links occur in reciprocal pairs,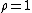 ; if r=0,
; if r=0, 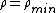 .
.
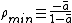
This is another advantage of using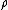 , because it incorporates the idea that complete antireciprocal is more statistical significant in the networks with larger density, while it has to be regarded as a less pronounced effect in sparser networks.
, because it incorporates the idea that complete antireciprocal is more statistical significant in the networks with larger density, while it has to be regarded as a less pronounced effect in sparser networks.
In different types of networks, has different relations with
has different relations with  and
and 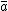 .
.
.
.
Clustering coefficient
In graph theory, a clustering coefficient is a measure of degree to which nodes in a graph tend to cluster together. Evidence suggests that in most real-world networks, and in particular social networks, nodes tend to create tightly knit groups characterised by a relatively high density of ties...
, scale-free
Scale-free network
A scale-free network is a network whose degree distribution follows a power law, at least asymptotically. That is, the fraction P of nodes in the network having k connections to other nodes goes for large values of k as...
degree distribution
Degree distribution
In the study of graphs and networks, the degree of a node in a network is the number of connections it has to other nodes and the degree distribution is the probability distribution of these degrees over the whole network.-Definition:...
, community structures, etc. Here Reciprocity is another quantity to specifically characterize directed networks
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
. Link reciprocity measures the tendency of vertex pairs to form mutual connections between each other.
Why we need to introduce it?
In real network problems, people are interested in determining the likelihoodLikelihood
Likelihood is a measure of how likely an event is, and can be expressed in terms of, for example, probability or odds in favor.-Likelihood function:...
of occurring double links (with opposite directions) between vertice pairs. This problem is fundamental for several
reasons. First, in the networks that transport information or material (such as email networks
, World Wide Web (WWW) , World Trade Web , or Wikipedia itself ), the mutual links will facilitate the transportation process. Second, when analyzing directed networks, people often treat them as undirected ones for simplicity; therefore the information obtained from reciprocity studies tells us how much is deviated from the truth when a directed network is treated as undirected (for example, when measuring the cluster coefficient). Finally, detecting
nontrivial patterns of reciprocity is interesting, since it can reveal possible mechanisms and organizing principles that shape the observed network topology.
Traditional definition
A traditional way to define the reciprocity r is using the ratio of the number of links pointing in both directions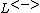 to the total number of links L
to the total number of links L 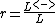
With this definition,
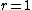 is for a purely bidirectional network while
is for a purely bidirectional network while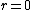 for a purely unidirectional one. Real networks have an intermediate value between 0 and 1.
for a purely unidirectional one. Real networks have an intermediate value between 0 and 1.However, this definition of reciprocity has some defects. It cannot tell the relative difference of reciprocity compared with purely random network with the same number of vertices and edges. The useful information from reciprocity is not the value itself, but whether mutual links occur more or less often than expected by chance. Besides, in those networks containing self-linking loops (links starting and ending at the same vertex), the self-linking loops should be excluded when calculating L.
Garlaschelli and Loffredo's definition
In order to overcome the defects of the above definition, Garlaschelli and Loffredo defined reciprocity as the correlation coefficient between the entries of the adjacency matrix of a directed graph (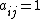 if a link from i to j is there, and
if a link from i to j is there, and 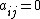 if not):
if not):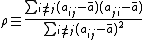 ,
,where the average value
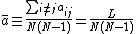 .
.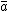 measures the ratio of observed to possible directed links (link density), and self-linking loops are now excluded from L because of i not equal to j.
measures the ratio of observed to possible directed links (link density), and self-linking loops are now excluded from L because of i not equal to j.The definition can be written in the following simple form:

The new definition of reciprocity gives an absolute quantity which directly allows one to distinguish between reciprocal (
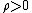 ) and antireciprocal (
) and antireciprocal (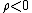 ) networks, with mutual links occurring more and less often than random respectively.
) networks, with mutual links occurring more and less often than random respectively.If all the links occur in reciprocal pairs,
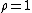 ; if r=0,
; if r=0, 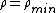 .
.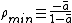
This is another advantage of using
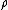 , because it incorporates the idea that complete antireciprocal is more statistical significant in the networks with larger density, while it has to be regarded as a less pronounced effect in sparser networks.
, because it incorporates the idea that complete antireciprocal is more statistical significant in the networks with larger density, while it has to be regarded as a less pronounced effect in sparser networks.Reciprocity for various types of networks
The following table shows the calculated values of reciprocity for various types of networks, from the result we can see that networks of same type displays similar value of reciprocity . Fig. 1 shows the reciprocity for three kinds of networks.In different types of networks,
 has different relations with
has different relations with  and
and 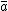 .
..
.

