Rational singularity
Encyclopedia
In mathematics
, more particularly in the field of algebraic geometry
, a scheme
has rational singularities, if it is normal
, of finite type over a field of characteristic zero, and there exists a proper birational map
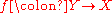
from a regular scheme
such that the higher direct images of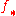 
applied to 
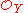are trivial. That is,
for 
.
If there is one such resolution, then it follows that all resolutions share this property, since any two resolutions of singularities can be dominated by a third.
For surfaces, rational singularities were defined by .
has rational singularities if and only if the natural map in the derived category
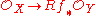
is a quasi-isomorphism
. Notice that this includes the statement that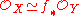
and hence the assumption that 
is normal.
There are related notions in positive and mixed characteristic of
and
Rational singularities are in particular Cohen-Macaulay
, normal
and Du Bois. They need not be Gorenstein
or even Q-Gorenstein.
Log terminal singularities are rational.
showed that
the rational double points of a algebraic surface
s are the Du Val singularities.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more particularly in the field of algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, a scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
has rational singularities, if it is normalNormal scheme
In mathematics, in the field of algebraic geometry, a normal scheme is a scheme X for which every stalk of its structure sheaf OX is an integrally closed local ring; that is, each stalk is an integral domain such that its integral closure in its field of fractions is equal to itself.Any reduced...
, of finite type over a field of characteristic zero, and there exists a proper birational map
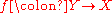
from a regular scheme
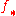such that the higher direct images of applied to 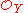are trivial. That is, for .If there is one such resolution, then it follows that all resolutions share this property, since any two resolutions of singularities can be dominated by a third.
For surfaces, rational singularities were defined by .
Formulations
Alternately, one can say that has rational singularities if and only if the natural map in the derived categoryDerived category
In mathematics, the derived category D of an abelian category C is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on C...
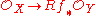
is a quasi-isomorphism
Quasi-isomorphism
In homological algebra, a branch of mathematics, a quasi-isomorphism is a morphism A → B of chain complexes such that the induced morphisms...
. Notice that this includes the statement that
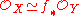and hence the assumption that is normal.There are related notions in positive and mixed characteristic of
- pseudo-rational
and
- F-rational
Rational singularities are in particular Cohen-Macaulay
Cohen-Macaulay ring
In mathematics, a Cohen–Macaulay ring is a particular type of commutative ring, possessing some of the algebraic-geometric properties of a nonsingular variety, such as local equidimensionality....
, normal
Normal scheme
In mathematics, in the field of algebraic geometry, a normal scheme is a scheme X for which every stalk of its structure sheaf OX is an integrally closed local ring; that is, each stalk is an integral domain such that its integral closure in its field of fractions is equal to itself.Any reduced...
and Du Bois. They need not be Gorenstein
Gorenstein ring
In commutative algebra, a Gorenstein local ring is a Noetherian commutative local ring R with finite injective dimension, as an R-module. There are many equivalent conditions, some of them listed below, most dealing with some sort of duality condition....
or even Q-Gorenstein.
Log terminal singularities are rational.
Examples
An example of a rational singularity is the singular point of the quadric coneshowed that
the rational double points of a algebraic surface
Algebraic surface
In mathematics, an algebraic surface is an algebraic variety of dimension two. In the case of geometry over the field of complex numbers, an algebraic surface has complex dimension two and so of dimension four as a smooth manifold.The theory of algebraic surfaces is much more complicated than that...
s are the Du Val singularities.