
Quasireversibility
Encyclopedia
In probability theory
, specifically queueing theory
, quasireversibility (sometimes QR) is a property of some queues. The concept was first identified by Richard R. Muntz and further developed by Frank Kelly
. Quasireversibility differs from reversibility in that a stronger condition is imposed on arrival rates and a weaker condition is applied on probability fluxes. For example, an M/M/1 queue with state-dependent arrival rates and state-dependent service times is reversible, but not quasireversible.
A network of queues, such that each individual queue when considered in isolation is quasireversible, always has a product form
stationary distribution.
 is quasireversible if its state at time t, x(t) is independent of
is quasireversible if its state at time t, x(t) is independent of
for all classes of customer.

then considering just customers of a particular class, the arrival and departure processes are the same Poisson process
(with parameter ), so
), so
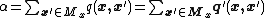
where Mx is a set such that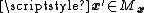 means the state x' represents a single arrival of the particular class of customer to state x.
means the state x' represents a single arrival of the particular class of customer to state x.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, specifically queueing theory
Queueing theory
Queueing theory is the mathematical study of waiting lines, or queues. The theory enables mathematical analysis of several related processes, including arriving at the queue, waiting in the queue , and being served at the front of the queue...
, quasireversibility (sometimes QR) is a property of some queues. The concept was first identified by Richard R. Muntz and further developed by Frank Kelly
Frank Kelly (professor)
Francis Patrick "Frank" Kelly, FRS is professor of the Mathematics of Systems in the Statistical Laboratory, University of Cambridge, and Master of Christ's College, Cambridge....
. Quasireversibility differs from reversibility in that a stronger condition is imposed on arrival rates and a weaker condition is applied on probability fluxes. For example, an M/M/1 queue with state-dependent arrival rates and state-dependent service times is reversible, but not quasireversible.
A network of queues, such that each individual queue when considered in isolation is quasireversible, always has a product form
Product form solution
In probability theory, a product form solution is a particularly efficient form of solution for determining some metric of a system with distinct sub-components, where the metric for the collection of components can be written as a product of the metric across the different components...
stationary distribution.
Definition
A queue with stationary distribution is quasireversible if its state at time t, x(t) is independent of
is quasireversible if its state at time t, x(t) is independent of- the arrival times for each class of customer subsequent to time t,
- the departure times for each class of customer prior to time t
for all classes of customer.
Partial balance formulation
Quasireversibility is equivalent to a particular form of partial balance. First, define the reversed rates q'(x,x') by
then considering just customers of a particular class, the arrival and departure processes are the same Poisson process
Poisson process
A Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
(with parameter
 ), so
), so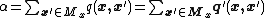
where Mx is a set such that
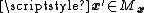 means the state x' represents a single arrival of the particular class of customer to state x.
means the state x' represents a single arrival of the particular class of customer to state x.Examples
- Burke's theoremBurke's theoremIn probability theory, Burke's theorem is a theorem in queueing theory by Paul J. Burke while working at Bell Telephone Laboratories that states for an M/M/1, M/M/m or M/M/∞ queue in the steady state with arrivals a Poisson process with rate parameter λ then:# The departure process is a Poisson...
shows that an M/M/m queueing system is quasireversible. - Kelly showed that each station of a BCMP networkBCMP networkIn queueing theory, a discipline within the mathematical theory of probability, a BCMP network is a class of queueing network for which a product form equilibrium distribution exists. It is named after the authors of the paper where the network was first described: Baskett, Chandy, Muntz and Palacios...
is quasireversible when viewed in isolation.

