Quasiprojective variety
Encyclopedia
In mathematics
, a quasiprojective variety in algebraic geometry
is a locally closed subset of a projective variety, i.e., the intersection inside some projective space
of a Zariski-open and a Zariski-closed subset. A similar definition is used in scheme theory, where a quasiprojective scheme is a locally closed subscheme of some projective space.
is a Zariski-open subset of projective space
, and since any closed affine subset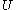
can be expressed as an intersection of the projective completion 
and the affine space embedded in the projective space, this implies that any affine variety is quasiprojective. There are locally closed subsets of projective space that are not affine, so that quasiprojective is more general than affine. Taking the complement of a single point in projective space of dimension at least 2 gives a non-affine quasiprojective variety. This is also an example of a quasiprojective variety that is neither affine nor projective.
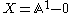, is isomorphic to the zero set of the polynomial 
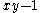in the affine plane. As an affine set X is not closed since any polynomial zero on the complement must be zero on the affine line. For another example, the complement of any conic in projective space of dimension 2 is affine. Varieties isomorphic to open subsets of affine varieties are called quasi-affine.
Quasiprojective varieties are locally affine in the sense that a manifold
is locally Euclidean — every point of a quasiprojective variety has a neighborhood given by an affine variety. This yields a basis of affine sets for the Zariski topology on a quasiprojective variety.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a quasiprojective variety in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
is a locally closed subset of a projective variety, i.e., the intersection inside some projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
of a Zariski-open and a Zariski-closed subset. A similar definition is used in scheme theory, where a quasiprojective scheme is a locally closed subscheme of some projective space.
Relationship to affine varieties
For example, affine spaceAffine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
is a Zariski-open subset of projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
, and since any closed affine subset
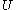can be expressed as an intersection of the projective completion and the affine space embedded in the projective space, this implies that any affine variety is quasiprojective. There are locally closed subsets of projective space that are not affine, so that quasiprojective is more general than affine. Taking the complement of a single point in projective space of dimension at least 2 gives a non-affine quasiprojective variety. This is also an example of a quasiprojective variety that is neither affine nor projective.Examples
Since quasiprojective varieties generalize both affine and projective varieties, they are sometimes referred to simply as varieties. Varieties isomorphic to affine algebraic varieties as quasiprojective varieties are called affine varieties; similarly for projective varieties. For example, the complement of a point in the affine line, i.e.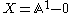, is isomorphic to the zero set of the polynomial 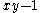in the affine plane. As an affine set X is not closed since any polynomial zero on the complement must be zero on the affine line. For another example, the complement of any conic in projective space of dimension 2 is affine. Varieties isomorphic to open subsets of affine varieties are called quasi-affine.Quasiprojective varieties are locally affine in the sense that a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
is locally Euclidean — every point of a quasiprojective variety has a neighborhood given by an affine variety. This yields a basis of affine sets for the Zariski topology on a quasiprojective variety.