Planar ternary ring
Encyclopedia
In mathematics
, a ternary ring is an algebraic structure
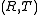consisting of a non-empty set 
and a ternary mapping 
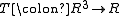, and a planar ternary ring (PTR) or ternary field is special sort of a ternary ring used by to give coordinates to projective plane
s. A planar ternary ring is not a ring
in the traditional sense.
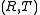where 
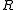is a nonempty set, containing distinct elements called 0 and 1, and 
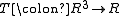satisfies these five axioms:
When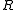
is finite, the third and fifth axioms are equivalent in the presence of the fourth.
No other pair (0',1') in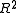
can be found such that 
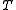still satisfies the first two axioms.
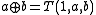. The structure 
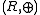turns out be a loop with identity element
0.
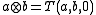. The set 
turns out be closed under this multiplication. The structure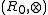 
also turns out to be a loop with identity element 1.
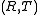is said to be linear if 
.
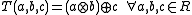For example, the planar ternary ring associated to a quasifield
is (by construction) linear.
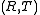, one can construct a projective plane
in this way (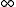
is a random symbol not in 
):
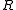One can prove that every projective plane is constructed in this way starting with a certain planar ternary ring. However, two nonisomorphic planar ternary rings can lead to the construction of isomorphic projective planes.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a ternary ring is an algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
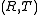consisting of a non-empty set and a ternary mapping 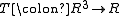, and a planar ternary ring (PTR) or ternary field is special sort of a ternary ring used by to give coordinates to projective planeProjective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
s. A planar ternary ring is not a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
in the traditional sense.
Definition
A planar ternary ring is a structu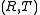re where 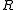is a nonempty set, containing distinct elements called 0 and 1, and 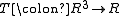satisfies these five axioms:
-
; -
; -
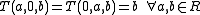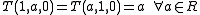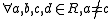, there is a unique 
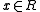such that : 
; -
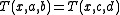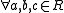, there is a unique 
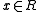, such that 
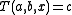; and -
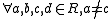, the equations 
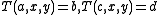have a unique solution 
.
When
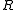is finite, the third and fifth axioms are equivalent in the presence of the fourth.No other pair (0',1') in
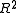can be found such that 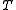still satisfies the first two axioms.Addition
Define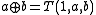. The structure 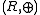turns out be a loop with identity elementIdentity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
0.
Multiplication
Define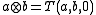. The set turns out be closed under this multiplication. The structure 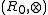also turns out to be a loop with identity element 1.Linear PTR
A planar ternary ring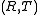 is said to be linear if 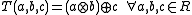.For example, the planar ternary ring associated to a quasifield
Quasifield
In mathematics, a quasifield is an algebraic structure where + and \cdot are binary operations on Q, much like a division ring, but with some weaker conditions.-Definition:A quasifield is a structure, where + and...
is (by construction) linear.
Connection with projective planes
Given a planar ternary ring, one can construct a projective planeProjective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
in this way (
is a random symbol not in ):
-
-
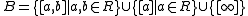
- We define the incidence relation
in this way (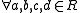
):
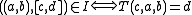
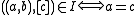
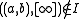
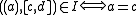
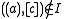
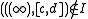
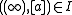
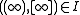
One can prove that every projective plane is constructed in this way starting with a certain planar ternary ring. However, two nonisomorphic planar ternary rings can lead to the construction of isomorphic projective planes.