Quasi-continuous function
Encyclopedia
In mathematics
, the notion of a quasi-continuous function is similar to, but weaker than, the notion of a continuous function
. All continuous functions are quasi-continuous but the converse is not true in general.
be a topological space
. A real-valued function
is quasi-continuous at a point 
if for any every 
and any open neighborhood 
of 
there is a non-empty open set
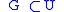such that
Note that in the above definition, it is not necessary that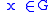
.
defined by 
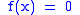whenever 
and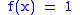 
whenever 
. Clearly f is continuous everywhere except at x=0, thus quasi-continuous everywhere except at x=0. At x=0, take any open neighborhood U of x. Then there exists an open set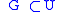 
such that 
. Clearly this yields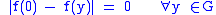 
thus f is quasi-continuous.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the notion of a quasi-continuous function is similar to, but weaker than, the notion of a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
. All continuous functions are quasi-continuous but the converse is not true in general.
Definition
Let be a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
. A real-valued function
is quasi-continuous at a point if for any every and any open neighborhood of there is a non-empty open setOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
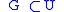such that
Note that in the above definition, it is not necessary that
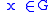.Properties
- If
is continuous then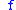 
is quasi-continuous - If
is continuous and 
is quasi-continuous, then 
is quasi-continuous.
Example
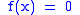Consider the function defined by whenever and 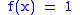whenever . Clearly f is continuous everywhere except at x=0, thus quasi-continuous everywhere except at x=0. At x=0, take any open neighborhood U of x. Then there exists an open set 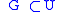such that . Clearly this yields 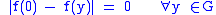thus f is quasi-continuous.