Quadratic Lie algebra
Encyclopedia
A quadratic Lie algebra is a Lie algebra
together with a compatible symmetric bilinear form. Compatibility means that it is invariant under the adjoint representation. Examples of such are semisimple Lie algebras, such as the su(n) and sl(n,R).
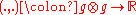that is invariant under the adjoint action, i.e.+(Y,[X,Z])=0
where X,Y,Z are elements of the Lie algebra g.
A localization/ generalization is the concept of Courant algebroid
where the vector space g is replaced by (sections of) a vector bundle
.
.
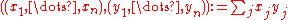Since the bracket is trivial the invariance is trivially fulfilled.
As a more elaborate example consider so(3), i.e. R3 with base X,Y,Z, standard inner product, and Lie bracket
.
Straightforward computation shows that the inner product is indeed preserved. A generalization is the following.
.
Define now the Killing form
.
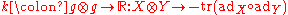Due to the Cartan criterion, the Killing form is non-degenerate if and only if the Lie algebra is semisimple.
If g is in addition a simple Lie algebra, then the Killing form is up to rescaling the only invariant symmetric bilinear form.
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
together with a compatible symmetric bilinear form. Compatibility means that it is invariant under the adjoint representation. Examples of such are semisimple Lie algebras, such as the su(n) and sl(n,R).
Definition
A quadratic Lie algebra is a Lie algebra (g,[.,.]) together with an inner product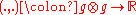 that is invariant under the adjoint action, i.e.+(Y,[X,Z])=0where X,Y,Z are elements of the Lie algebra g.
A localization/ generalization is the concept of Courant algebroid
Courant algebroid
In a field of mathematics known as differential geometry, a Courant algebroid is a combination of a Lie algebroid and a quadratic Lie algebra. It was originally introduced in 1990 by Theodore James Courant in his dissertation at UC Berkeley where he first called them Dirac Manifolds, and then were...
where the vector space g is replaced by (sections of) a vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
.
Examples
As a first example, consider Rn with zero-bracket and standard inner product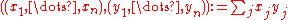.Since the bracket is trivial the invariance is trivially fulfilled.
As a more elaborate example consider so(3), i.e. R3 with base X,Y,Z, standard inner product, and Lie bracket
.Straightforward computation shows that the inner product is indeed preserved. A generalization is the following.
Semisimple Lie algebras
A big group of examples fits into the category of semisimple Lie algebras, i.e. Lie algebras whose adjoint representation is faithful. Examples are sl(n,R) and su(n), as well as direct sums of them. Let thus g be a semi-simple Lie algebra with adjoint representation ad, i.e..Define now the Killing form
Killing form
In mathematics, the Killing form, named after Wilhelm Killing, is a symmetric bilinear form that plays a basic role in the theories of Lie groups and Lie algebras...
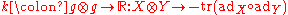.Due to the Cartan criterion, the Killing form is non-degenerate if and only if the Lie algebra is semisimple.
If g is in addition a simple Lie algebra, then the Killing form is up to rescaling the only invariant symmetric bilinear form.