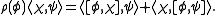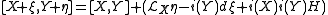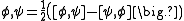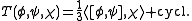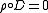Courant algebroid
Encyclopedia
In a field of mathematics
known as differential geometry, a Courant algebroid is a combination of a Lie algebroid
and a quadratic Lie algebra
. It was originally introduced in 1990 by Theodore James Courant
in his dissertation at UC Berkeley where he first called them Dirac Manifolds, and then were re-named after him in 1997 by Zhang-Ju Liu, Alan Weinstein
and Ping Xu to describe the double of a Lie bialgebroid.
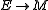with a bracket 
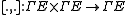, a non degenerate inner product 
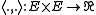, and a bundle map 
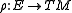subject to the following axioms,
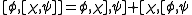
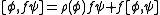
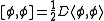
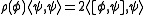
where φ,ψ are sections into E and f is a smooth function on the base manifold M. D is the combination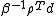
with d the de Rham differential, 
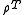the dual map of 
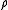, and β the map from E to 
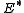induced by the metric.
The fourth rule is an invariance of the inner product under the bracket. Polarization leads to
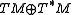with a twist introduced by Ševera, defined as:
where X,Y are vector fields, ξ,η are 1-forms and H is a closed 3-form twisting the bracket. This bracket is used to describe the integrability of generalized complex structures.
A more general example arises from a Lie algebroid A whose induced differential on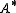
will be written as d again. Then use the same formula as for the Dorfman bracket with H an A-3-form closed under d.
Another example of a Courant algebroid is a quadratic Lie algebra, i.e. a Lie algebra with an invariant scalar product. Here the base manifold is just a point and thus the anchor map (and D) are trivial.
The example described in the paper by Weinstein et al. comes from a Lie bialgebroid, i.e. A a Lie algebroid (with anchor
and bracket 
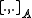), also its dual 
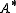a Lie algebroid (inducing the differential 
on 
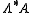) and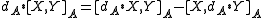 
(where on the RHS you extend the A-bracket to 
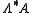using graded Leibniz rule). This notion is symmetric in A and 
(see Roytenberg). Here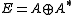 
with anchor 
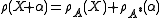and the bracket is the skew-symmetrization of the above in X and α (equivalently in Y and β):
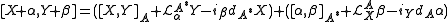
This fulfils a homotopic Jacobi-identity.
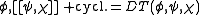
where T is
The Leibniz rule and the invariance of the scalar product become modified by the relation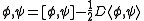
and the violation of skew-symmetry gets replaced by the axiom
The skew-symmetric bracket together with the derivation D and the Jacobiator T form a strongly homotopic Lie algebra.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
known as differential geometry, a Courant algebroid is a combination of a Lie algebroid
Lie algebroid
In mathematics, Lie algebroids serve the same role in the theory of Lie groupoids that Lie algebras serve in the theory of Lie groups: reducing global problems to infinitesimal ones...
and a quadratic Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
. It was originally introduced in 1990 by Theodore James Courant
Theodore James Courant
Theodore James Courant is a mathematician who has conducted research in the fields of differential geometry and classical mechanics. In particular, he made seminal contributions to the study of Dirac manifolds, which generalize both symplectic manifolds and Poisson manifolds, and are related to...
in his dissertation at UC Berkeley where he first called them Dirac Manifolds, and then were re-named after him in 1997 by Zhang-Ju Liu, Alan Weinstein
Alan Weinstein
Alan David Weinstein is a professor of mathematics at the University of California, Berkeley who works in symplectic geometry, Poisson Geometry and Mathematical Physics....
and Ping Xu to describe the double of a Lie bialgebroid.
Definition
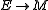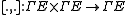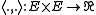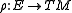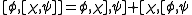
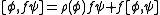
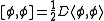
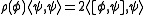
A Courant algebroid consists of the data a vector bundle with a bracket , a non degenerate inner product , and a bundle map subject to the following axioms,where φ,ψ are sections into E and f is a smooth function on the base manifold M. D is the combination
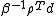with d the de Rham differential, 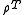the dual map of 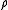, and β the map from E to 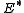induced by the metric.Properties
The bracket is not skew-symmetric as one can see from the third axiom. Instead it fulfils a certain Jacobi-identity (first axiom) and a Leibniz rule (second axiom). From these two axioms one can derive that the anchor map ρ is a morphism of brackets:
The fourth rule is an invariance of the inner product under the bracket. Polarization leads to
Examples
An example of the Courant algebroid is the Dorfman bracket on the direct sum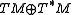 with a twist introduced by Ševera, defined as:
where X,Y are vector fields, ξ,η are 1-forms and H is a closed 3-form twisting the bracket. This bracket is used to describe the integrability of generalized complex structures.
A more general example arises from a Lie algebroid A whose induced differential on
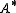will be written as d again. Then use the same formula as for the Dorfman bracket with H an A-3-form closed under d.Another example of a Courant algebroid is a quadratic Lie algebra, i.e. a Lie algebra with an invariant scalar product. Here the base manifold is just a point and thus the anchor map (and D) are trivial.
The example described in the paper by Weinstein et al. comes from a Lie bialgebroid, i.e. A a Lie algebroid (with anchor
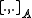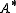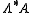and bracket ), also its dual a Lie algebroid (inducing the differential on ) and 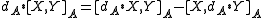(where on the RHS you extend the A-bracket to 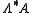using graded Leibniz rule). This notion is symmetric in A and (see Roytenberg). Here 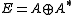with anchor 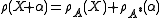and the bracket is the skew-symmetrization of the above in X and α (equivalently in Y and β):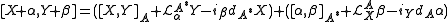Skew-symmetric bracket
Instead of the definition above one can introduce a skew-symmetric bracket as
This fulfils a homotopic Jacobi-identity.
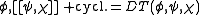
where T is
The Leibniz rule and the invariance of the scalar product become modified by the relation
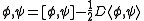and the violation of skew-symmetry gets replaced by the axiom
The skew-symmetric bracket together with the derivation D and the Jacobiator T form a strongly homotopic Lie algebra.