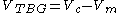Q-guidance
Encyclopedia
Q-guidance is a method of missile guidance
used in some U.S. ballistic missiles and some civilian space flights. It was developed in the 1950's by J. Halcombe Laning
and Richard Battin at the MIT Instrumentation Lab
.
Q-guidance is used for missiles whose trajectory consists of a relatively short boost phase
(or powered phase) during which the missile's propulsion system operates, followed by a ballistic phase during which the missile coasts to its target under the influence of gravity. (Cruise missile
s use different guidance methods). The objective of Q-guidance is to hit a specified target at a specified time (if there is some flexibility as to the time the target should be hit then other types of guidance can be used).
I and II used Delta-guidance, while Q-guidance was used for Thor IRBM and Polaris, and presumably Poseidon. It appears, from monitoring of test launches, that early Soviet ICBMs used a variant of Delta-guidance.
expansion around the reference trajectory. The guidance system attempt to zero the linear terms of this expression, i.e. to bring the missile back to the pre-planned trajectory. For this reason Delta-guidance is sometimes referred to as "fly [along] the wire", where the (imaginary) wire refers to the reference trajectory.
In contrast Q-guidance is a dynamic method, reminiscent of the theories dynamic programming
or state based feedback
. In essence it says "never mind where we were supposed to be, given where we are what should we do to make progress towards the goal of reaching the required target at the required time". To do this is relies on the concept of "velocity to be gained".
The actual velocity of the missile is denoted by Vm and the missile is subject to both the acceleration due to gravity g and that due to the engines aT. the velocity to be gained is defined as the difference between Vc and Vm:
A simple guidance strategy is to apply acceleration (i.e. engine thrust) in the direction of VTBG. This will have the effect of making the actual velocity come closer to Vc. When they become equal (i.e. when VTBG becomes identically zero) it is time to shut off the engines, since the missile is by definition able to reach the desired target at the desired time on its own.
The only remaining issue is how to compute VTBG easily from information available on board the vehicle.
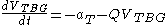
where the Q matrix is defined by
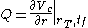
where Q is a symmetric 3 by 3 time-varying matrix. (The vertical bar refers to the fact that the derivative must be evaluated for a given target position rT and time of free flight tf). The calculation of this matrix is non-trivial, but can be performed offline before the flight; experience shows that the matrix is only slowly time varying, so only a few values of Q corresponding to different times during the flight need to be stored on board the vehicle.
In early applications the integration of the differential equation was performed using analog hardware, rather than a digital computer. Information about vehicle acceleration, velocity and position is supplied by the onboard Inertial measurement unit
.
Derivation of the equation
Notation:
t the current time
r the current vehicle position vector
Vm the current vehicle velocity vector
T the time the vehicle will reach the target
tf the time of free flight for the correlated vehicle, i.e. t-T
[...]
where
is a constant. This implicitly assumes that VTBG remains roughly constant during the maneuver. A somewhat more clever strategy can be designed that takes into account the rate of time change of VTBG as well, since this is available from the differential equation above.
This second control strategy is based on Battin's insight that "If you want to drive a vector to zero, it is [expedient] to align the time rate of change of the vector with the vector itself". This suggests setting the auto-pilot steering rate to
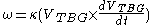
Either of these methods are referred to as cross-product steering, and they are easy to implement in analog hardware.
Finally, when all components of VTBG are small, the order to cut-off engine power can be given.
Guidance system
A guidance system is a device or group of devices used to navigate a ship, aircraft, missile, rocket, satellite, or other craft. Typically, this refers to a system that navigates without direct or continuous human control...
used in some U.S. ballistic missiles and some civilian space flights. It was developed in the 1950's by J. Halcombe Laning
J. Halcombe Laning
Dr. J. Halcombe "Hal" Laning Jr. was a Massachusetts Institute of Technology computer pioneer who in 1952 invented an algebraic compiler called George that ran on the MIT Whirlwind, the first real-time computer...
and Richard Battin at the MIT Instrumentation Lab
Charles Stark Draper Laboratory
Draper Laboratory is an American not-for-profit research and development organization in Cambridge, Massachusetts. Draper focuses on the design, development, and deployment of advanced technology solutions to problems in national security, space exploration, health care and energy.Originally...
.
Q-guidance is used for missiles whose trajectory consists of a relatively short boost phase
Boost phase
The boost phase is the portion of the flight of a ballistic missile or space vehicle during which the booster and sustainer engines operate until it reaches peak velocity. This phase can take 3 to 4 minutes , the altitude at the end of this phase is 150–200 km, and the typical burn-out speed...
(or powered phase) during which the missile's propulsion system operates, followed by a ballistic phase during which the missile coasts to its target under the influence of gravity. (Cruise missile
Cruise missile
A cruise missile is a guided missile that carries an explosive payload and is propelled, usually by a jet engine, towards a land-based or sea-based target. Cruise missiles are designed to deliver a large warhead over long distances with high accuracy...
s use different guidance methods). The objective of Q-guidance is to hit a specified target at a specified time (if there is some flexibility as to the time the target should be hit then other types of guidance can be used).
Early Implementations
At the time Q-guidance was developed the main competitive method was called Delta-guidance. According to Mackenzie, Titan, some versions of Atlas, MinutemanLGM-30 Minuteman
The LGM-30 Minuteman is a U.S. nuclear missile, a land-based intercontinental ballistic missile . As of 2010, the version LGM-30G Minuteman-III is the only land-based ICBM in service in the United States...
I and II used Delta-guidance, while Q-guidance was used for Thor IRBM and Polaris, and presumably Poseidon. It appears, from monitoring of test launches, that early Soviet ICBMs used a variant of Delta-guidance.
Delta-guidance overview
This is not the place for a detailed discussion of Delta-guidance; suffice it to say that it is based on adherence to a pre-planned trajectory. Using ground-based computers a reference trajectory is developed before the flight and stored in the missile's guidance system. In flight, the actual trajectory is modeled mathematically as a Taylor seriesTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
expansion around the reference trajectory. The guidance system attempt to zero the linear terms of this expression, i.e. to bring the missile back to the pre-planned trajectory. For this reason Delta-guidance is sometimes referred to as "fly [along] the wire", where the (imaginary) wire refers to the reference trajectory.
In contrast Q-guidance is a dynamic method, reminiscent of the theories dynamic programming
Dynamic programming
In mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
or state based feedback
State space (controls)
In control engineering, a state space representation is a mathematical model of a physical system as a set of input, output and state variables related by first-order differential equations...
. In essence it says "never mind where we were supposed to be, given where we are what should we do to make progress towards the goal of reaching the required target at the required time". To do this is relies on the concept of "velocity to be gained".
Velocity To Be Gained
At a given time t and for a given vehicle position r, the correlated velocity vector Vc is defined as follows: if the vehicle had the velocity Vc and the propulsion system was turned off, then the missile would reach the desired target at the desired time under the influence of gravity. In some sense, Vc is the desired velocity.The actual velocity of the missile is denoted by Vm and the missile is subject to both the acceleration due to gravity g and that due to the engines aT. the velocity to be gained is defined as the difference between Vc and Vm:
A simple guidance strategy is to apply acceleration (i.e. engine thrust) in the direction of VTBG. This will have the effect of making the actual velocity come closer to Vc. When they become equal (i.e. when VTBG becomes identically zero) it is time to shut off the engines, since the missile is by definition able to reach the desired target at the desired time on its own.
The only remaining issue is how to compute VTBG easily from information available on board the vehicle.
The Q Matrix
A remarkably simple differential equation can be used to compute the velocity to be gained: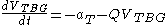where the Q matrix is defined by
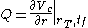
where Q is a symmetric 3 by 3 time-varying matrix. (The vertical bar refers to the fact that the derivative must be evaluated for a given target position rT and time of free flight tf). The calculation of this matrix is non-trivial, but can be performed offline before the flight; experience shows that the matrix is only slowly time varying, so only a few values of Q corresponding to different times during the flight need to be stored on board the vehicle.
In early applications the integration of the differential equation was performed using analog hardware, rather than a digital computer. Information about vehicle acceleration, velocity and position is supplied by the onboard Inertial measurement unit
Inertial measurement unit
An inertial measurement unit, or IMU, is an electronic device that measures and reports on a craft's velocity, orientation, and gravitational forces, using a combination of accelerometers and gyroscopes. IMUs are typically used to maneuver aircraft, including UAVs, among many others, and...
.
Derivation of the equation
Notation:
t the current time
r the current vehicle position vector
Vm the current vehicle velocity vector
T the time the vehicle will reach the target
tf the time of free flight for the correlated vehicle, i.e. t-T
[...]
Cross Product Steering
A reasonable strategy to gradually align the thrust vector to the VTBG vector is to steer at a rate proportional to the cross product between them. A simple control strategy that does this is to steer at the ratewhere
is a constant. This implicitly assumes that VTBG remains roughly constant during the maneuver. A somewhat more clever strategy can be designed that takes into account the rate of time change of VTBG as well, since this is available from the differential equation above.This second control strategy is based on Battin's insight that "If you want to drive a vector to zero, it is [expedient] to align the time rate of change of the vector with the vector itself". This suggests setting the auto-pilot steering rate to
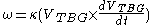
Either of these methods are referred to as cross-product steering, and they are easy to implement in analog hardware.
Finally, when all components of VTBG are small, the order to cut-off engine power can be given.