
Pseudotensor
Encyclopedia
In physics
and mathematics
, a pseudotensor is usually a quantity that transforms like a tensor
under an orientation preserving coordinate transformation (e.g., a proper rotation), but gains an additional sign flip under an orientation reversing coordinate transformation (e.g., an improper rotation
, which is a transformation that can be expressed as an inversion followed by a proper rotation).
There is a second meaning for pseudotensor, restricted to general relativity
; tensors obey strict transformation laws, whilst pseudotensors are not so constrained. Consequently the form of a pseudotensor will, in general, change as the frame of reference is altered. An equation which holds in a frame containing pseudotensors will not necessarily hold in a different frame; this makes pseudotensors of limited relevance because equations in which they appear are not invariant
in form.
The first context is essentially a tensor multiplied by an extra sign factor, such that the pseudotensor changes sign under reflections when a normal tensor does not. According to one definition, a pseudotensor P of the type (p,q) is a geometric object whose components in an arbitrary basis are enumerated by (p + q) indices and obey the transformation rule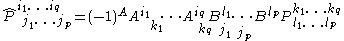
under a change of basis.
Here are the components of the pseudotensor in the new and old bases, respectively,
are the components of the pseudotensor in the new and old bases, respectively, 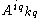 is the transition matrix for the contravariant indices,
is the transition matrix for the contravariant indices, 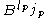 is the transition matrix for the covariant indices, and
is the transition matrix for the covariant indices, and 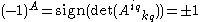 .
.
This transformation rule differs from the rule for an ordinary tensor in the intermediate treatment only by the presence of the factor (-1)A.
The second context where the word "pseudotensor" is used is General Relativity
. In that theory, one cannot describe the energy and momentum of the gravitational field by an energy-momentum tensor. Instead, one introduces objects that behave as tensors only with respect to restricted coordinate transformations. Strictly speaking, such objects are not tensors at all. A famous example of such a pseudotensor is the Landau-Lifshitz pseudotensor.
due to the non-orientability, but one can define a volume element
, which is formally a density
, and may also be called a pseudo-volume form, due to the additional sign twist (tensoring with the sign bundle).
A change of variable
s in multi-dimensional integration is achieved by incorporation of a factor of the absolute value of the determinant of the Jacobian matrix. The use of the absolute value introduces a sign-flip for improper coordinate transformations; as such, an integrand is an example of a pseudotensor density according to the first definition.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a pseudotensor is usually a quantity that transforms like a tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
under an orientation preserving coordinate transformation (e.g., a proper rotation), but gains an additional sign flip under an orientation reversing coordinate transformation (e.g., an improper rotation
Improper rotation
In 3D geometry, an improper rotation, also called rotoreflection or rotary reflection is, depending on context, a linear transformation or affine transformation which is the combination of a rotation about an axis and a reflection in a plane perpendicular to the axis.Equivalently it is the...
, which is a transformation that can be expressed as an inversion followed by a proper rotation).
There is a second meaning for pseudotensor, restricted to general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
; tensors obey strict transformation laws, whilst pseudotensors are not so constrained. Consequently the form of a pseudotensor will, in general, change as the frame of reference is altered. An equation which holds in a frame containing pseudotensors will not necessarily hold in a different frame; this makes pseudotensors of limited relevance because equations in which they appear are not invariant
Covariance and contravariance
In multilinear algebra and tensor analysis, covariance and contravariance describe how the quantitative description of certain geometric or physical entities changes with a change of basis from one coordinate system to another. When one coordinate system is just a rotation of the other, this...
in form.
Definition
Two quite different mathematical objects are called a pseudotensor in different contexts.The first context is essentially a tensor multiplied by an extra sign factor, such that the pseudotensor changes sign under reflections when a normal tensor does not. According to one definition, a pseudotensor P of the type (p,q) is a geometric object whose components in an arbitrary basis are enumerated by (p + q) indices and obey the transformation rule
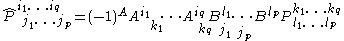
under a change of basis.
Here
 are the components of the pseudotensor in the new and old bases, respectively,
are the components of the pseudotensor in the new and old bases, respectively, 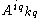 is the transition matrix for the contravariant indices,
is the transition matrix for the contravariant indices, 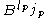 is the transition matrix for the covariant indices, and
is the transition matrix for the covariant indices, and 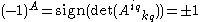 .
.This transformation rule differs from the rule for an ordinary tensor in the intermediate treatment only by the presence of the factor (-1)A.
The second context where the word "pseudotensor" is used is General Relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
. In that theory, one cannot describe the energy and momentum of the gravitational field by an energy-momentum tensor. Instead, one introduces objects that behave as tensors only with respect to restricted coordinate transformations. Strictly speaking, such objects are not tensors at all. A famous example of such a pseudotensor is the Landau-Lifshitz pseudotensor.
Examples
On non-orientable manifolds, one cannot define a volume formVolume form
In mathematics, a volume form on a differentiable manifold is a nowhere-vanishing differential form of top degree. Thus on a manifold M of dimension n, a volume form is an n-form, a section of the line bundle Ωn = Λn, that is nowhere equal to zero. A manifold has a volume...
due to the non-orientability, but one can define a volume element
Volume element
In mathematics, a volume element provides a means for integrating a function with respect to volume in various coordinate systems such as spherical coordinates and cylindrical coordinates...
, which is formally a density
Density on a manifold
In mathematics, and specifically differential geometry, a density is a spatially varying quantity on a differentiable manifold which can be integrated in an intrinsic manner. Abstractly, a density is a section of a certain trivial line bundle, called the density bundle...
, and may also be called a pseudo-volume form, due to the additional sign twist (tensoring with the sign bundle).
A change of variable
Integration by substitution
In calculus, integration by substitution is a method for finding antiderivatives and integrals. Using the fundamental theorem of calculus often requires finding an antiderivative. For this and other reasons, integration by substitution is an important tool for mathematicians...
s in multi-dimensional integration is achieved by incorporation of a factor of the absolute value of the determinant of the Jacobian matrix. The use of the absolute value introduces a sign-flip for improper coordinate transformations; as such, an integrand is an example of a pseudotensor density according to the first definition.
See also
- TensorTensorTensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
- Tensor densityTensor densityIn differential geometry, a tensor density or relative tensor is a generalization of the tensor concept. A tensor density transforms as a tensor when passing from one coordinate system to another , except that it is additionally multiplied or weighted by a power of the Jacobian determinant of the...
- General relativityGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
- Noether's theoremNoether's theoremNoether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...
- PseudovectorPseudovectorIn physics and mathematics, a pseudovector is a quantity that transforms like a vector under a proper rotation, but gains an additional sign flip under an improper rotation such as a reflection. Geometrically it is the opposite, of equal magnitude but in the opposite direction, of its mirror image...
- Variational principleVariational principleA variational principle is a scientific principle used within the calculus of variations, which develops general methods for finding functions which minimize or maximize the value of quantities that depend upon those functions...
- Conservation lawConservation lawIn physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves....
- Action (physics)Action (physics)In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...

