
Pseudo-determinant
Encyclopedia
In linear algebra
and statistics
, the pseudo-determinant is the product of all non-zero eigenvalues of a square matrix. It coincides with the regular determinant
when the matrix is non-singular.
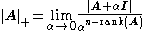
where |A| denotes the usual determinant
, I denotes the identity matrix
and rank(A) denotes the rank
of A.
, then the singular values
and eigenvalues of A coincide. In this case, if the singular value decomposition
(SVD) is available, then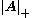 may be computed as the product of the non-zero singular values. If all singular values are zero, then the pseudo-determinant is 1.
may be computed as the product of the non-zero singular values. If all singular values are zero, then the pseudo-determinant is 1.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the pseudo-determinant is the product of all non-zero eigenvalues of a square matrix. It coincides with the regular determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
when the matrix is non-singular.
Definition
The pseudo-determinant of a square n-by-n matrix A may be defined as: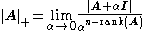
where |A| denotes the usual determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
, I denotes the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
and rank(A) denotes the rank
Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
of A.
Computation for positive semi-definite case
If A is positive semi-definitePositive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
, then the singular values
Singular value decomposition
In linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
and eigenvalues of A coincide. In this case, if the singular value decomposition
Singular value decomposition
In linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
(SVD) is available, then
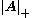 may be computed as the product of the non-zero singular values. If all singular values are zero, then the pseudo-determinant is 1.
may be computed as the product of the non-zero singular values. If all singular values are zero, then the pseudo-determinant is 1.Application in statistics
If a statistical procedure ordinarily compares distributions in terms of the determinants of variance-covariance matrices then, in the case of singular matrices, this comparison can be undertaken by using a combination of the ranks of the matrices and their pseudo-determinants, with the matrix of higher rank being counted as "largest" and the pseudo-determinants only being used if the ranks are equal. Thus pseudo-determinants are sometime presented in the outputs of statistical programs in cases where covariance matrices are singular.See also
- Matrix determinant
- Moore-Penrose pseudoinverse, which can also be obtained in terms of the non-zero singular values.

