Product integral
Encyclopedia
Product integrals are a counterpart of standard integral
s of infinitesimal calculus. They were first developed by the mathematician Vito Volterra
in 1887 to solve systems of linear differential equations. Since then, product integrals have found use in areas from epidemiology
(the Kaplan–Meier estimator) to stochastic population dynamics (multigrals), analysis and quantum mechanics
.
Examples of product integrals are the geometric integral (see below) and the bigeometric integral. (Although those two integrals are multiplicative, the concepts of product integral and multiplicative integral are not the same).
This article adopts the "product"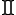
notation for product integration instead of the "integral" 
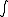(usually modified by a superimposed "times" symbol or letter P) favoured by Volterra and others. An arbitrary classification of types is also adopted to impose some order in the field.
It is when applied to functions of a non-commutative variable such as matrix function
s that product integrals offers something different - In the commutative case, calculations can be done using workarounds with the usual additive calculus operators.
of a function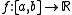
can be defined by the relation
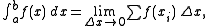
where the limit
is taken over all partitions of interval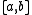
whose norm approach zero.
Product integrals are similar, but take the limit of a product instead of the limit of a sum.
They can be thought of as "continuous" versions of "discrete" products.
The most popular product integrals are the following:
\exp\left(\int_a^b \ln f(x) \, dx\right),
which is called the "geometric integral" and is a multiplicative operator.
This definition of the product integral is the continuous equivalent of the discrete product operator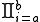
(with 
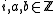) and the multiplicative equivalent to the (normal/standard/additive) integral 
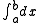(with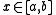 
):
It is very useful in stochastics where the log-likelihood (i.e. the logarithm of a product integral of independent random variables) equals the integral of the log of the these (infinitesimally many) random variables:
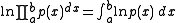
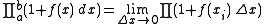
Under these definitions, a real function is product integrable if and only if it is Riemann integrable. There are other more general definitions such as the Lebesgue product integral, Riemann–Stieltjes product integral, or Henstock–Kurzweil product integral.
The second type corresponds to Volterra's original definition. The following relationship exists for scalar functions
:
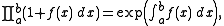
which is not a multiplicative operator. However, this type of product integral is most useful when applied to matrix-valued functions or functions with values in a Banach algebra, where the last equality is no longer true (see the references below).
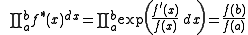
where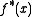
is the "geometric derivative".
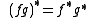
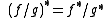
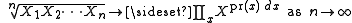
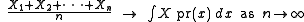
The above are for Type I Product integrals. Other types produce other results.
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
s of infinitesimal calculus. They were first developed by the mathematician Vito Volterra
Vito Volterra
Vito Volterra was an Italian mathematician and physicist, known for his contributions to mathematical biology and integral equations....
in 1887 to solve systems of linear differential equations. Since then, product integrals have found use in areas from epidemiology
Epidemiology
Epidemiology is the study of health-event, health-characteristic, or health-determinant patterns in a population. It is the cornerstone method of public health research, and helps inform policy decisions and evidence-based medicine by identifying risk factors for disease and targets for preventive...
(the Kaplan–Meier estimator) to stochastic population dynamics (multigrals), analysis and quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
.
Examples of product integrals are the geometric integral (see below) and the bigeometric integral. (Although those two integrals are multiplicative, the concepts of product integral and multiplicative integral are not the same).
This article adopts the "product"
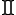notation for product integration instead of the "integral" 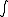(usually modified by a superimposed "times" symbol or letter P) favoured by Volterra and others. An arbitrary classification of types is also adopted to impose some order in the field.It is when applied to functions of a non-commutative variable such as matrix function
Matrix function
In mathematics, a matrix function is a function which maps a matrix to another matrix.- Extending scalar functions to matrix functions :There are several techniques for lifting a real function to a square matrix function such that interesting properties are maintained...
s that product integrals offers something different - In the commutative case, calculations can be done using workarounds with the usual additive calculus operators.
Basic definitions
The classical Riemann integralRiemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
of a function
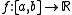can be defined by the relation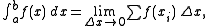where the limit
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
is taken over all partitions of interval
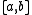whose norm approach zero.Product integrals are similar, but take the limit of a product instead of the limit of a sum.
They can be thought of as "continuous" versions of "discrete" products.
The most popular product integrals are the following:
\exp\left(\int_a^b \ln f(x) \, dx\right),
which is called the "geometric integral" and is a multiplicative operator.
This definition of the product integral is the continuous equivalent of the discrete product operator
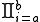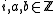(with ) and the multiplicative equivalent to the (normal/standard/additive) integral 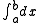(with 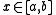):| additive | multiplicative | |
| discrete |  |
 |
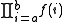| continuous |  |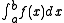
 |
It is very useful in stochastics where the log-likelihood (i.e. the logarithm of a product integral of independent random variables) equals the integral of the log of the these (infinitesimally many) random variables:
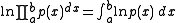
Type II
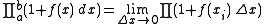
Under these definitions, a real function is product integrable if and only if it is Riemann integrable. There are other more general definitions such as the Lebesgue product integral, Riemann–Stieltjes product integral, or Henstock–Kurzweil product integral.
The second type corresponds to Volterra's original definition. The following relationship exists for scalar functions
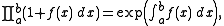
:which is not a multiplicative operator. However, this type of product integral is most useful when applied to matrix-valued functions or functions with values in a Banach algebra, where the last equality is no longer true (see the references below).
Results
The geometric integral (Type I above) plays a central role in the "geometric calculus", which is a multiplicative calculus.- The fundamental theorem
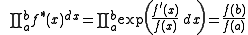
where
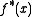is the "geometric derivative".- Product rule
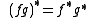
- Quotient rule
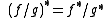
- Law of large numbers
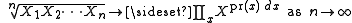
- where X is a random variable with probability distribution pr(x)).
- Compare with the standard Law of Large Numbers:
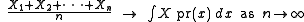
The above are for Type I Product integrals. Other types produce other results.
External links
- Richard Gill, Product Integration
- Richard Gill, Product Integral Symbol
- David Manura, Product Calculus
- Tyler Neylon, Easy bounds for n!
- An Introduction to Multigral (Product) and Dx-less Calculus
- Notes On the Lax equation
- Antonín Slavík, An introduction to product integration
- Antonín Slavík, Henstock–Kurzweil and McShane product integration