Probabilistic logic
Encyclopedia
The aim of a probabilistic logic (or probability logic) is to combine the capacity of probability theory
to handle uncertainty with the capacity of deductive logic to exploit structure. The result is a richer and more expressive formalism with a broad range of possible application areas. Probabilistic logic is a natural extension of traditional logic truth tables: the results they define are derived through probabilistic expressions instead. The difficulty with probabilistic logics is that they tend to multiply the computational complexities of their probabilistic and logical components.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
to handle uncertainty with the capacity of deductive logic to exploit structure. The result is a richer and more expressive formalism with a broad range of possible application areas. Probabilistic logic is a natural extension of traditional logic truth tables: the results they define are derived through probabilistic expressions instead. The difficulty with probabilistic logics is that they tend to multiply the computational complexities of their probabilistic and logical components.
Proposals
There are numerous proposals for probabilistic logics:- The term "probabilistic logic" was first used in a paper by Nils Nilsson published in 1986, where the truth values of sentences are probabilities. The proposed semantical generalization induces a probabilistic logical entailmentEntailmentIn logic, entailment is a relation between a set of sentences and a sentence. Let Γ be a set of one or more sentences; let S1 be the conjunction of the elements of Γ, and let S2 be a sentence: then, Γ entails S2 if and only if S1 and not-S2 are logically inconsistent...
, which reduces to ordinary logical entailmentEntailmentIn logic, entailment is a relation between a set of sentences and a sentence. Let Γ be a set of one or more sentences; let S1 be the conjunction of the elements of Γ, and let S2 be a sentence: then, Γ entails S2 if and only if S1 and not-S2 are logically inconsistent...
when the probabilities of all sentences are either 0 or 1. This generalization applies to any logical system for which the consistency of a finite set of sentences can be established. - In the theory of probabilistic argumentationProbabilistic argumentationThe name "probabilistic argumentation" has been used to refer to a particular theory of reasoning that encompasses uncertainty and ignorance, combining probability theory and deductive logic, and thus consisting in a probabilistic logic ....
, probabilities are not directly attached to logical sentences. Instead it is assumed that a particular subset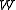
of the variables 
involved in the sentences defines a probability spaceProbability spaceIn probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
over the corresponding sub-σ-algebra. This induces two distinct probability measures with respect to
, which are called degree of support and degree of possibility, respectively. Degrees of support can be regarded as non-additive probabilities of provability, which generalizes the concepts of ordinary logical entailmentEntailmentIn logic, entailment is a relation between a set of sentences and a sentence. Let Γ be a set of one or more sentences; let S1 be the conjunction of the elements of Γ, and let S2 be a sentence: then, Γ entails S2 if and only if S1 and not-S2 are logically inconsistent...
(for
) and classical posterior probabilitiesPosterior probabilityIn Bayesian statistics, the posterior probability of a random event or an uncertain proposition is the conditional probability that is assigned after the relevant evidence is taken into account...
(for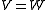
). Mathematically, this view is compatible with the Dempster-Shafer theoryDempster-Shafer theoryThe Dempster–Shafer theory is a mathematical theory of evidence. It allows one to combine evidence from different sources and arrive at a degree of belief that takes into account all the available evidence. The theory was first developed by Arthur P...
. - The theory of evidential reasoningEvidential reasoningEvidential reason or evidential reasoning may refer to:* Probabilistic logic, a combination of the capacity of probability theory to handle uncertainty with the capacity of deductive logic to exploit structure...
also defines non-additive probabilities of probability (or epistemic probabilities) as a general notion for both logical entailmentEntailmentIn logic, entailment is a relation between a set of sentences and a sentence. Let Γ be a set of one or more sentences; let S1 be the conjunction of the elements of Γ, and let S2 be a sentence: then, Γ entails S2 if and only if S1 and not-S2 are logically inconsistent...
(provability) and probabilityProbabilityProbability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
. The idea is to augment standard propositional logic by considering an epistemic operator K that represents the state of knowledge that a rational agent has about the world. Probabilities are then defined over the resulting epistemic universe Kp of all propositional sentences p, and it is argued that this is the best information available to an analyst. From this view, Dempster-Shafer theoryDempster-Shafer theoryThe Dempster–Shafer theory is a mathematical theory of evidence. It allows one to combine evidence from different sources and arrive at a degree of belief that takes into account all the available evidence. The theory was first developed by Arthur P...
appears to be a generalized form of probabilistic reasoning. - Approximate reasoning formalism proposed by fuzzy logicFuzzy logicFuzzy logic is a form of many-valued logic; it deals with reasoning that is approximate rather than fixed and exact. In contrast with traditional logic theory, where binary sets have two-valued logic: true or false, fuzzy logic variables may have a truth value that ranges in degree between 0 and 1...
can be used to obtain a logic in which the models are the probability distributions and the theories are the lower envelopes. In such a logic the question of the consistency of the available information is strictly related with the one of the coherence of partial probabilistic assignment and therefore with Dutch bookDutch bookIn gambling a Dutch book or lock is a set of odds and bets which guarantees a profit, regardless of the outcome of the gamble. It is associated with probabilities implied by the odds not being coherent....
phenomenon. - The central concept in the theory of subjective logicSubjective logicSubjective logic is a type of probabilistic logic that explicitly takes uncertainty and belief ownership into account. In general, subjective logic is suitable for modeling and analysing situations involving uncertainty and incomplete knowledge...
are opinions about some of the propositional variablePropositional variableIn mathematical logic, a propositional variable is a variable which can either be true or false...
s involved in the given logical sentences. A binomial opinion applies to a single proposition and is represented as a 3-dimensional extension of a single probability value to express various degrees of ignorance about the truth of the proposition. For the computation of derived opinions based on a structure of argument opinions, the theory proposes respective operators for various logical connectives, such as e.g. multiplication (ANDLogical conjunctionIn logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
), comultiplication (ORLogical disjunctionIn logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
), division (UN-AND) and co-division (UN-OR) of opinions as well as conditional deduction (MPModus ponensIn classical logic, modus ponendo ponens or implication elimination is a valid, simple argument form. It is related to another valid form of argument, modus tollens. Both Modus Ponens and Modus Tollens can be mistakenly used when proving arguments...
) and abduction (MTModus tollensIn classical logic, modus tollens has the following argument form:- Formal notation :...
) . - Markov logic networkMarkov logic networkA Markov logic network is a probabilistic logic which applies the ideas of a Markov network to first-order logic, enabling uncertain inference...
s implement a form of uncertain inferenceUncertain inferenceUncertain inference was first described by Rijsbergen as a way to formally define a query and document relationship in Information retrieval. This formalization is a logical implication with an attached measure of uncertainty.-Definitions:...
based on the maximum entropy principle -- the idea that probabilities should be assigned in such a way as to maximize entropy, in analogy with the way that Markov chainMarkov chainA Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
s assign probabilities to finite state machineFinite state machineA finite-state machine or finite-state automaton , or simply a state machine, is a mathematical model used to design computer programs and digital logic circuits. It is conceived as an abstract machine that can be in one of a finite number of states...
transitions. - Probabilistic logic networkProbabilistic logic networkA probabilistic logic network is a novel conceptual, mathematical and computational approach to uncertain inference; inspired by logic programming, but using probabilities in place of crisp truth values, and fractional uncertainty in place of crisp known/unknown values...
s is an implementation of a probilistic logic system, using techniques and algorithms from logic programmingLogic programmingLogic programming is, in its broadest sense, the use of mathematical logic for computer programming. In this view of logic programming, which can be traced at least as far back as John McCarthy's [1958] advice-taker proposal, logic is used as a purely declarative representation language, and a...
and other systems.
Possible application areas
- Argumentation theoryArgumentation theoryArgumentation theory, or argumentation, is the interdisciplinary study of how humans should, can, and do reach conclusions through logical reasoning, that is, claims based, soundly or not, on premises. It includes the arts and sciences of civil debate, dialogue, conversation, and persuasion...
- Artificial intelligenceArtificial intelligenceArtificial intelligence is the intelligence of machines and the branch of computer science that aims to create it. AI textbooks define the field as "the study and design of intelligent agents" where an intelligent agent is a system that perceives its environment and takes actions that maximize its...
- BioinformaticsBioinformaticsBioinformatics is the application of computer science and information technology to the field of biology and medicine. Bioinformatics deals with algorithms, databases and information systems, web technologies, artificial intelligence and soft computing, information and computation theory, software...
- Formal epistemologyFormal epistemologyFormal epistemology uses formal methods from decision theory, logic, probability theory and computability theory to elucidate epistemic problems. Work in this area spans several academic fields, including philosophy, computer science, economics, and statistics...
- Game theoryGame theoryGame theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
- Philosophy of sciencePhilosophy of scienceThe philosophy of science is concerned with the assumptions, foundations, methods and implications of science. It is also concerned with the use and merit of science and sometimes overlaps metaphysics and epistemology by exploring whether scientific results are actually a study of truth...
- PsychologyPsychologyPsychology is the study of the mind and behavior. Its immediate goal is to understand individuals and groups by both establishing general principles and researching specific cases. For many, the ultimate goal of psychology is to benefit society...
- StatisticsStatisticsStatistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
See also
- Statistical relational learningStatistical relational learningStatistical relational learning is a subdiscipline of artificial intelligence and machine learning that is concerned with models of domains that exhibit both uncertainty and complex, relational structure...
- Bayesian inferenceBayesian inferenceIn statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
, Bayesian networks, Bayesian probabilityBayesian probabilityBayesian probability is one of the different interpretations of the concept of probability and belongs to the category of evidential probabilities. The Bayesian interpretation of probability can be seen as an extension of logic that enables reasoning with propositions, whose truth or falsity is... - Cox's theoremCox's theoremCox's theorem, named after the physicist Richard Threlkeld Cox, is a derivation of the laws of probability theory from a certain set of postulates. This derivation justifies the so-called "logical" interpretation of probability. As the laws of probability derived by Cox's theorem are applicable to...
- Dempster-Shafer theoryDempster-Shafer theoryThe Dempster–Shafer theory is a mathematical theory of evidence. It allows one to combine evidence from different sources and arrive at a degree of belief that takes into account all the available evidence. The theory was first developed by Arthur P...
- Fuzzy logicFuzzy logicFuzzy logic is a form of many-valued logic; it deals with reasoning that is approximate rather than fixed and exact. In contrast with traditional logic theory, where binary sets have two-valued logic: true or false, fuzzy logic variables may have a truth value that ranges in degree between 0 and 1...
- Imprecise probabilityImprecise probabilityImprecise probability generalizes probability theory to allow for partial probability specifications, and is applicable when information is scarce, vague, or conflicting, in which case a unique probability distribution may be hard to identify...
- LogicLogicIn philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, Deductive logic, Non-monotonic logicNon-monotonic logicA non-monotonic logic is a formal logic whose consequence relation is not monotonic. Most studied formal logics have a monotonic consequence relation, meaning that adding a formula to a theory never produces a reduction of its set of consequences. Intuitively, monotonicity indicates that learning a... - Probabilistic databaseProbabilistic databaseA probabilistic database is an uncertain database in which the possible worlds have associated probabilities. Probabilistic database management systems are currently an active area of research...
- ProbabilityProbabilityProbability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
, Probability theoryProbability theoryProbability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single... - Probabilistic argumentationProbabilistic argumentationThe name "probabilistic argumentation" has been used to refer to a particular theory of reasoning that encompasses uncertainty and ignorance, combining probability theory and deductive logic, and thus consisting in a probabilistic logic ....
- Reasoning
- Subjective logicSubjective logicSubjective logic is a type of probabilistic logic that explicitly takes uncertainty and belief ownership into account. In general, subjective logic is suitable for modeling and analysing situations involving uncertainty and incomplete knowledge...
- UncertaintyUncertaintyUncertainty is a term used in subtly different ways in a number of fields, including physics, philosophy, statistics, economics, finance, insurance, psychology, sociology, engineering, and information science...
- Upper and lower probabilitiesUpper and lower probabilitiesUpper and lower probabilities are representations of imprecise probability. Whereas probability theory uses a single number, the probability, to describe how likely an event is to occur, this method uses two numbers: the upper probability of the event and the lower probability of the event.Because...
Further reading
- Adams, E. W., 1998. A Primer of Probability Logic. CSLI Publications (Univ. of Chicago Press).
- Bacchus, F., 1990. "Representing and reasoning with Probabilistic Knowledge. A Logical Approach to Probabilities". The MIT Press.
- Carnap, R.Rudolf CarnapRudolf Carnap was an influential German-born philosopher who was active in Europe before 1935 and in the United States thereafter. He was a major member of the Vienna Circle and an advocate of logical positivism....
, 1950. Logical Foundations of Probability. University of Chicago Press. - Chuaqui, R., 1991. Truth, Possibility and Probability: New Logical Foundations of Probability and Statistical Inference. Number 166 in Mathematics Studies. North-Holland.
- Hájek, A., 2001, "Probability, Logic, and Probability Logic," in Goble, Lou, ed., The Blackwell Guide to Philosophical Logic, Blackwell.
- Kyburg, H. E.Henry E. Kyburg, Jr.Henry E. Kyburg, Jr. was Gideon Burbank Professor of Moral Philosophy and Professor of Computer Science at the University of Rochester, New York, and Pace Eminent Scholar at the Institute for Human and Machine Cognition, Pensacola, Florida...
, 1970. Probability and Inductive Logic Macmillan. - Kyburg, H. E., 1974. The Logical Foundations of Statistical Inference, Dordrecht: Reidel.
- Kyburg, H. E. & C. M. Teng, 2001. Uncertain Inference, Cambridge: Cambridge University Press.
- Romeiyn, J. W., 2005. Bayesian Inductive Logic. PhD thesis, Faculty of Philosophy, University of Groningen, Netherlands. http://www.philos.rug.nl/~romeyn/paper/2005_romeijn_-_thesis.pdf
- Williamson, J., 2002, "Probability Logic," in D. Gabbay, R. Johnson, H. J. Ohlbach, and J. Woods, eds., Handbook of the Logic of Argument and Inference: the Turn Toward the Practical. Elsevier: 397-424.