
Prime constant
Encyclopedia
The prime constant is the real number
 whose
whose  th binary digit is 1 if
th binary digit is 1 if  is prime
is prime
and 0 if n is composite
or 1.
In other words, is simply the number whose binary expansion
is simply the number whose binary expansion
corresponds to the indicator function of the set of prime number
s. That is,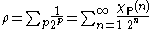
where indicates a prime and
indicates a prime and  is the characteristic function of the primes.
is the characteristic function of the primes.
The beginning of the decimal expansion of ρ is: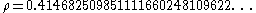
The beginning of the binary expansion is:
 is easily shown to be irrational
is easily shown to be irrational
. To see why, suppose it were rational.
Denote the th digit of the binary expansion of
th digit of the binary expansion of 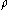 by
by  . Then, since
. Then, since  is assumed rational, there must exist
is assumed rational, there must exist  ,
, 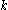 positive integers such that
positive integers such that
 for all
for all  and all
and all 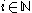 .
.
Since there are an infinite number of primes, we may choose a prime . By definition we see that
. By definition we see that  . As noted, we have
. As noted, we have 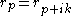 for all
for all  . Now consider the case
. Now consider the case  . We have
. We have 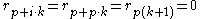 , since
, since  is composite because
is composite because 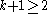 . Since
. Since 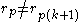 we see that
we see that  is irrational.
is irrational.
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
 whose
whose  th binary digit is 1 if
th binary digit is 1 if  is prime
is primePrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
and 0 if n is composite
Composite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
or 1.
In other words,
 is simply the number whose binary expansion
is simply the number whose binary expansionBinary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
corresponds to the indicator function of the set of prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s. That is,
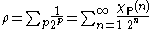
where
 indicates a prime and
indicates a prime and  is the characteristic function of the primes.
is the characteristic function of the primes.The beginning of the decimal expansion of ρ is:
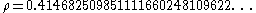
The beginning of the binary expansion is:

Irrationality
The number is easily shown to be irrational
is easily shown to be irrationalIrrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
. To see why, suppose it were rational.
Denote the
 th digit of the binary expansion of
th digit of the binary expansion of 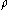 by
by  . Then, since
. Then, since  is assumed rational, there must exist
is assumed rational, there must exist  ,
, 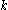 positive integers such that
positive integers such that for all
for all  and all
and all 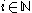 .
.Since there are an infinite number of primes, we may choose a prime
 . By definition we see that
. By definition we see that  . As noted, we have
. As noted, we have 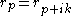 for all
for all  . Now consider the case
. Now consider the case  . We have
. We have 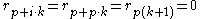 , since
, since  is composite because
is composite because 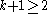 . Since
. Since 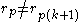 we see that
we see that  is irrational.
is irrational.

