
Primary pseudoperfect number
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and particularly in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, a primary pseudoperfect number is a number N that satisfies the Egyptian fraction equation
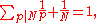
where the sum is over only the prime divisors of N. Equivalently (as can be seen by multiplying this equation by N),

Except for the exceptional primary pseudoperfect number 2, this expression gives a representation for N as a sum of a set of distinct divisors of N; therefore each such number (except 2) is pseudoperfect
Semiperfect number
In number theory, a semiperfect number or pseudoperfect number is a natural number n that is equal to the sum of all or some of its proper divisors. A semiperfect number that is equal to the sum of all its proper divisors is a perfect number....
.
Primary pseudoperfect numbers were first investigated and named by Butske, Jaje, and Mayernik (2000). The first few primary pseudoperfect numbers are
- 2, 6, 4242 (number)42 is the natural number immediately following 41 and directly preceding 43. The number has received considerable attention in popular culture as a result of its central appearance in The Hitchhiker's Guide to the Galaxy as the "Answer to the Ultimate Question of Life, the Universe, and...
, 1806, 47058, 2214502422, 52495396602, ... .
The first four of these numbers are one less than the corresponding numbers in Sylvester's sequence
Sylvester's sequence
In number theory, Sylvester's sequence is an integer sequence in which each member of the sequence is the product of the previous members, plus one. The first few terms of the sequence are:...
but later numbers in Sylvester's sequence do not similarly correspond to primary pseudoperfect numbers. It is unknown whether there are infinitely many primary pseudoperfect numbers, or whether there are any odd primary pseudoperfect numbers.
The prime factors of primary pseudoperfect numbers may provide solutions to Znám's problem
Znám's problem
In number theory, Znám's problem asks which sets of k integers have the property that each integer in the set is a proper divisor of the product of the other integers in the set, plus 1. Znám's problem is named after the Slovak mathematician Štefan Znám, who suggested it in 1972, although other...
in which all members of the solution set are prime. For instance, the factors of the primary pseudoperfect number 47058 are the solution set {2,3,11,23,31} to Znám's problem. However, the smaller primary pseudoperfect numbers 2, 6, 42, and 1806 do not correspond to solutions to Znám's problem in this way, as their sets of prime factors violate the requirement in Znám's problem that no number in the set can equal one plus the product of all the other numbers. Anne (1998) observes that there is exactly one solution set of this type that has k primes in it, for each k ≤ 8, and conjectures that the same is true for larger k.
If a primary pseudoperfect number N is one less than a prime number, then N×(N+1) is also primary pseudoperfect. For instance, 47058 is primary pseudoperfect, and 47059 is prime, so 47058 × 47059 = 2214502422 is also primary pseudoperfect.
See also Giuga number
Giuga number
A Giuga number is a composite number n such that for each of its distinct prime factors pi we have p_i | , or equivalently such that for each of its distinct prime factors pi we have p_i^2 | ....
.

