
Pregaussian class
Encyclopedia
In probability theory
, a pregaussian class or pregaussian set of functions is a set of functions, square integrable with respect to some probability measure
, such that there exists a certain Gaussian process
, indexed by this set, satisfying the conditions below.
(S, Σ, P), denote by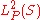 a set of square integrable with respect to P functions
a set of square integrable with respect to P functions  , that is
, that is
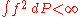
Consider a set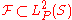 . There exists a Gaussian process
. There exists a Gaussian process
 , indexed by
, indexed by 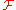 , with mean 0 and covariance
, with mean 0 and covariance
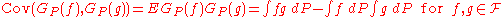
Such a process exists because the given covariance is positive definite. This covariance defines a semi-inner product as well as a pseudometric
on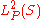 given by
given by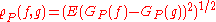
Definition A class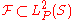 is called pregaussian if for each
is called pregaussian if for each 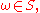 the function
the function  on
on 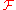 is bounded,
is bounded, 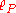 -uniformly continuous, and prelinear.
-uniformly continuous, and prelinear.
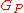 process is a generalization of the brownian bridge
process is a generalization of the brownian bridge
. Consider with P being the uniform measure
with P being the uniform measure
. In this case, the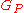 process indexed by the indicator functions
process indexed by the indicator functions 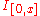 , for
, for  is in fact the standard brownian bridge
is in fact the standard brownian bridge
B(x). This set of the indicator functions is pregaussian, moreover, it is the Donsker class.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, a pregaussian class or pregaussian set of functions is a set of functions, square integrable with respect to some probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
, such that there exists a certain Gaussian process
Gaussian process
In probability theory and statistics, a Gaussian process is a stochastic process whose realisations consist of random values associated with every point in a range of times such that each such random variable has a normal distribution...
, indexed by this set, satisfying the conditions below.
Definition
For a probability spaceProbability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
(S, Σ, P), denote by
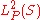 a set of square integrable with respect to P functions
a set of square integrable with respect to P functions  , that is
, that is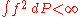
Consider a set
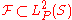 . There exists a Gaussian process
. There exists a Gaussian processGaussian process
In probability theory and statistics, a Gaussian process is a stochastic process whose realisations consist of random values associated with every point in a range of times such that each such random variable has a normal distribution...
 , indexed by
, indexed by 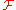 , with mean 0 and covariance
, with mean 0 and covariance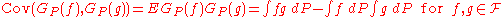
Such a process exists because the given covariance is positive definite. This covariance defines a semi-inner product as well as a pseudometric
Pseudometric space
In mathematics, a pseudometric space is a generalized metric space in which the distance between two distinct points can be zero. In the same way as every normed space is a metric space, every seminormed space is a pseudometric space...
on
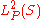 given by
given by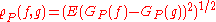
Definition A class
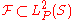 is called pregaussian if for each
is called pregaussian if for each 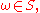 the function
the function  on
on 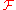 is bounded,
is bounded, 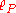 -uniformly continuous, and prelinear.
-uniformly continuous, and prelinear.Brownian bridge
The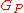 process is a generalization of the brownian bridge
process is a generalization of the brownian bridgeBrownian bridge
A Brownian bridge is a continuous-time stochastic process B whose probability distribution is the conditional probability distribution of a Wiener process W given the condition that B = B = 0.The expected value of the bridge is zero, with variance t, implying that the most...
. Consider
 with P being the uniform measure
with P being the uniform measureUniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
. In this case, the
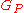 process indexed by the indicator functions
process indexed by the indicator functions 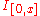 , for
, for  is in fact the standard brownian bridge
is in fact the standard brownian bridgeBrownian bridge
A Brownian bridge is a continuous-time stochastic process B whose probability distribution is the conditional probability distribution of a Wiener process W given the condition that B = B = 0.The expected value of the bridge is zero, with variance t, implying that the most...
B(x). This set of the indicator functions is pregaussian, moreover, it is the Donsker class.

