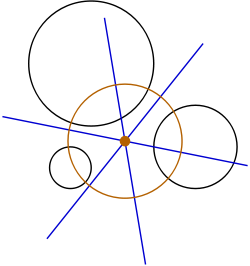
Power center
Encyclopedia
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the power center of three circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
s, also called the radical center, is the intersection point of the three radical axes
Radical axis
The radical axis of two circles is the locus of points at which tangents drawn to both circles have the same length. For any point P on the radical axis, there is a unique circle centered on P that intersects both circles at right angles ; conversely, the center of any circle that cuts both...
of the pairs of circles. If the radical center lies outside of all three circles, then it is the center of the unique circle (the radical circle) that intersects the three given circles orthogonally; the construction of this orthogonal circle corresponds to Monge's problem. This is a special case of the three conics theorem.
The three radical axes meet in a single point, the radical center, for the following reason. The radical axis of a pair of circles is defined as the set of points that have equal power
Power of a point
In elementary plane geometry, the power of a point is a real number h that reflects the relative distance of a given point from a given circle. Specifically, the power of a point P with respect to a circle C of radius r is defined...
h with respect to both circles. For example, for every point P on the radical axis of circles 1 and 2, the powers to each circle are equal, h1 = h2. Similarly, for every point on the radical axis of circles 2 and 3, the powers must be equal, h2 = h3. Therefore, at the intersection point of these two lines, all three powers must be equal, h1 = h2 = h3. Since this implies that h1 = h3, this point must also lie on the radical axis of circles 1 and 3. Hence, all three radical axes pass through the same point, the radical center.
The radical center has several applications in geometry. It has an important role in a solution to Apollonius' problem
Problem of Apollonius
In Euclidean plane geometry, Apollonius' problem is to construct circles that are tangent to three given circles in a plane . Apollonius of Perga posed and solved this famous problem in his work ; this work has been lost, but a 4th-century report of his results by Pappus of Alexandria has survived...
published by Joseph Diaz Gergonne
Joseph Diaz Gergonne
Joseph Diaz Gergonne was a French mathematician and logician.-Life:In 1791, Gergonne enlisted in the French army as a captain. That army was undergoing rapid expansion because the French government feared a foreign invasion intended to undo the French Revolution and restore Louis XVI to full power...
in 1814. Several types of radical circles have been defined as well, such as the radical circle of the Lucas circles.
External links
- Radical Center at Cut-the-KnotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Radical Axis and Center at Cut-the-KnotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...

