
Potential game
Encyclopedia
A game in game theory
is considered a potential game if the incentive of all players to change their strategy
can be expressed in one global function, the potential function. The concept was proposed by Dov Monderer and Lloyd Shapley
. Games can be either ordinal or cardinal potential games. In cardinal games, the difference in individual payoff
s for each player from individually changing one's strategy ceteris paribus
has to have the same value as the difference in values for the potential function. In ordinal games, only the signs of the differences have to be the same.
The potential function is a useful tool to analyze equilibrium properties of games, since the incentives of all players are mapped into one function, and the set of pure Nash equilibria
can be found by locating the local optima of the potential function.
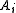 of each player and u the payoff function.
of each player and u the payoff function.
Then, a game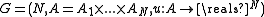 is a (cardinal) potential game if there is an exact potential function
is a (cardinal) potential game if there is an exact potential function 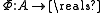 such that
such that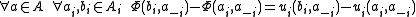
A game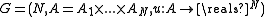 is a general (ordinal) potential game if there is an ordinal potential function
is a general (ordinal) potential game if there is an ordinal potential function 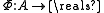 such that
such that
where sign denotes the Sign function
.
from choosing the same strategy. The strategy choices are +1 and −1, as seen in the payoff matrix in Figure 1.
This game has a potential function = .
If player 1 moves from −1 to +1, the payoff difference is Δu1 = = .
The change in potential is ΔP = = = = Δu1.
The solution for player 2 is equivalent. Using numerical values b1 = 2, b2 = −1, w = 3, this example transforms into a simple battle of the sexes
, as shown in Figure 2. The game has two pure Nash equilibria, (+1, +1) and (−1, −1). These are also the local maxima of the potential function (Figure 3). The only stochastically stable equilibrium
is (+1, +1), the global maximum of the potential function.
A 2-player, 2-strategy game is cannot be a potential game unless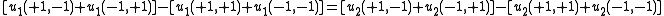
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
is considered a potential game if the incentive of all players to change their strategy
Strategy (game theory)
In game theory, a player's strategy in a game is a complete plan of action for whatever situation might arise; this fully determines the player's behaviour...
can be expressed in one global function, the potential function. The concept was proposed by Dov Monderer and Lloyd Shapley
Lloyd Shapley
Lloyd Stowell Shapley is a distinguished American mathematician and economist. He is a Professor Emeritus at University of California, Los Angeles, affiliated with departments of Mathematics and Economics...
. Games can be either ordinal or cardinal potential games. In cardinal games, the difference in individual payoff
Payoff
Payoff may refer to:* Bribery* A payoff dominant equilibrium in game theory* Payoff matrix or payoff function in a normal form game in game theory* Payoff set in set theory* Payoff, a 1991 TV film starring Keith Carradine...
s for each player from individually changing one's strategy ceteris paribus
Ceteris paribus
or is a Latin phrase, literally translated as "with other things the same," or "all other things being equal or held constant." It is an example of an ablative absolute and is commonly rendered in English as "all other things being equal." A prediction, or a statement about causal or logical...
has to have the same value as the difference in values for the potential function. In ordinal games, only the signs of the differences have to be the same.
The potential function is a useful tool to analyze equilibrium properties of games, since the incentives of all players are mapped into one function, and the set of pure Nash equilibria
Nash equilibrium
In game theory, Nash equilibrium is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally...
can be found by locating the local optima of the potential function.
Definition
Formally, let N be the number of players, A the set of action profiles over the action sets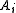 of each player and u the payoff function.
of each player and u the payoff function.Then, a game
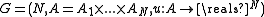 is a (cardinal) potential game if there is an exact potential function
is a (cardinal) potential game if there is an exact potential function 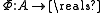 such that
such that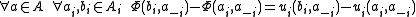
A game
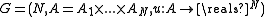 is a general (ordinal) potential game if there is an ordinal potential function
is a general (ordinal) potential game if there is an ordinal potential function 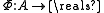 such that
such that
where sign denotes the Sign function
Sign function
In mathematics, the sign function is an odd mathematical function that extracts the sign of a real number. To avoid confusion with the sine function, this function is often called the signum function ....
.
A simple example
In a 2-player, 2-strategy game with externalities, individual players' payoffs are given by the function = , where si is players i's strategy, is the opponent's strategy, and w is a positive externalityExternality
In economics, an externality is a cost or benefit, not transmitted through prices, incurred by a party who did not agree to the action causing the cost or benefit...
from choosing the same strategy. The strategy choices are +1 and −1, as seen in the payoff matrix in Figure 1.
This game has a potential function = .
If player 1 moves from −1 to +1, the payoff difference is Δu1 = = .
The change in potential is ΔP = = = = Δu1.
The solution for player 2 is equivalent. Using numerical values b1 = 2, b2 = −1, w = 3, this example transforms into a simple battle of the sexes
Battle of the sexes (game theory)
In game theory, battle of the sexes , also called Bach or Stravinsky, is a two-player coordination game. Imagine a couple that agreed to meet this evening, but cannot recall if they will be attending the opera or a football match. The husband would most of all like to go to the football game. The...
, as shown in Figure 2. The game has two pure Nash equilibria, (+1, +1) and (−1, −1). These are also the local maxima of the potential function (Figure 3). The only stochastically stable equilibrium
Stochastically stable equilibrium
In game theory, a stochastically stable equilibrium is a refinement of the evolutionarily stable state in evolutionary game theory, proposed by Dean Foster and Peyton Young...
is (+1, +1), the global maximum of the potential function.
A 2-player, 2-strategy game is cannot be a potential game unless
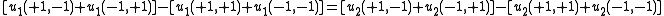
External links
- Lecture notes of Yishay Mansour about Potential and congestion games

