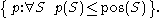Possibility theory
Encyclopedia
Possibility theory is a mathematical theory for dealing with certain types of uncertainty
and is an alternative to probability theory
. Professor Lotfi Zadeh first introduced possibility theory in 1978 as an extension of his theory of fuzzy sets and fuzzy logic
. D. Dubois
and H. Prade further contributed to its development. Earlier in the 50s, economist G.L.S. Shackle proposed the min/max algebra to describe degrees of potential surprise.
from Ω to [0, 1] such that:
It follows that, like probability, the possibility measure on finite set is determined by its behavior on singletons:
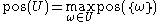
provided U is finite or countably infinite.
Axiom 1 can be interpreted as the assumption that Ω is an exhaustive description of future states of the world, because it means that no belief weight is given to elements outside Ω.
Axiom 2 could be interpreted as the assumption that the evidence from which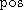
was constructed is free of any contradiction. Technically, it implies that there is at least one element in Ω with possibility 1.
Axiom 3 corresponds to the additivity axiom in probabilities. However there is an important practical difference. Possibility theory is computationally more convenient because Axioms 1-3 imply that:
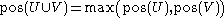for any subsets 
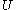and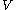 
.
Because one can know the possibility of the union from the possibility of each component, it can be said that possibility is compositional
with respect to the union operator. Note however that it is not compositional with respect to the intersection operator. Generally:
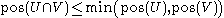
Remark for the mathematicians:
When Ω is not finite Axiom 3 can be replaced by:
uses a single number, the probability, to describe how likely an event is to occur, possibility theory uses two concepts, the possibility and the necessity of the event. For any set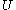
, the necessity measure is defined by
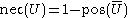
In the above formula,
denotes the complement of 
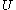, that is the elements of 
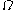that do not belong to 
. It is straightforward to show that:
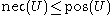for any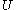 
and that:
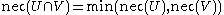
Note that contrary to probability theory, possibility is not self-dual. That is, for any event
, we only have the inequality:
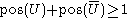
However, the following duality rule holds:
Accordingly, beliefs about an event can be represented by a number and a bit.
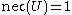means that 
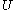is necessary. 
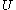is certainly true. It implies that 
.
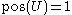means that 
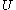is impossible. 
is certainly false. It implies that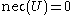 
.
means that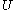 
is possible. I would not be surprised at all if 
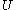occurs. It leaves 
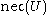unconstrained.
means that 
is unnecessary. I would not be surprised at all if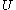 
does not occur. It leaves 
unconstrained.
The intersection of the last two cases is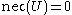
and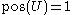 
meaning that I believe nothing at all about 
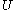. Because it allows for indeterminacy like this, possibility theory relates to the graduation of a many-valued logic, such as intuitionistic logic
, rather than the classical two-valued logic.
Note that unlike possibility, fuzzy logic is compositional with respect to both the union and the intersection operator. The relationship with fuzzy theory can be explained with the following classical example.
A possibility measure can be seen as a consonant plausibility measure in Dempster–Shafer theory
of evidence. The operators of possibility theory can be seen as a hyper-cautious version of the operators of the transferable belief model
, a modern development of the theory of evidence.
Possibility can be seen as an upper probability
: any possibility distribution defines a unique set of admissible probability distributions by
This allows one to study possibility theory using the tools of imprecise probabilities
.
. Also, there is only a fuzzy inference rule extending the usual Modus Ponens. Such a rule says that if α and α → β are proved at degree λ and μ, respectively, then we can assert β at degree min{λ,μ}. It is easy to see that the theories of such a logic are the generalized necessities and that the completely consistent theories coincide with the necessities (see for example Gerla 2001).
Uncertainty
Uncertainty is a term used in subtly different ways in a number of fields, including physics, philosophy, statistics, economics, finance, insurance, psychology, sociology, engineering, and information science...
and is an alternative to probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
. Professor Lotfi Zadeh first introduced possibility theory in 1978 as an extension of his theory of fuzzy sets and fuzzy logic
Fuzzy logic
Fuzzy logic is a form of many-valued logic; it deals with reasoning that is approximate rather than fixed and exact. In contrast with traditional logic theory, where binary sets have two-valued logic: true or false, fuzzy logic variables may have a truth value that ranges in degree between 0 and 1...
. D. Dubois
Didier Dubois
Didier Dubois is a French mathematician.Since 1999, he is a co-editor-in-chief of the journal Fuzzy Sets and Systems.In 1993–1997 he was vice-president and president of the International Fuzzy Systems Association....
and H. Prade further contributed to its development. Earlier in the 50s, economist G.L.S. Shackle proposed the min/max algebra to describe degrees of potential surprise.
Formalization of possibility
For simplicity, assume that the universe of discourse Ω is a finite set, and assume that all subsets are measurable. A distribution of possibility is a function from Ω to [0, 1] such that:- Axiom 1:
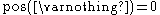
- Axiom 2:
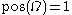
- Axiom 3:
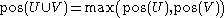for any disjoint subsets 
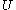and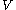 
.
It follows that, like probability, the possibility measure on finite set is determined by its behavior on singletons:
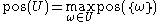
provided U is finite or countably infinite.
Axiom 1 can be interpreted as the assumption that Ω is an exhaustive description of future states of the world, because it means that no belief weight is given to elements outside Ω.
Axiom 2 could be interpreted as the assumption that the evidence from which
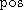was constructed is free of any contradiction. Technically, it implies that there is at least one element in Ω with possibility 1.Axiom 3 corresponds to the additivity axiom in probabilities. However there is an important practical difference. Possibility theory is computationally more convenient because Axioms 1-3 imply that:
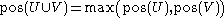for any subsets 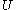and 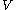.Because one can know the possibility of the union from the possibility of each component, it can be said that possibility is compositional
Principle of compositionality
In mathematics, semantics, and philosophy of language, the Principle of Compositionality is the principle that the meaning of a complex expression is determined by the meanings of its constituent expressions and the rules used to combine them. This principle is also called Frege's Principle,...
with respect to the union operator. Note however that it is not compositional with respect to the intersection operator. Generally:
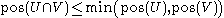
Remark for the mathematicians:
When Ω is not finite Axiom 3 can be replaced by:
- For all index sets
, if the subsets 
are pairwise disjoint,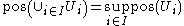 
Necessity
Whereas probability theoryProbability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
uses a single number, the probability, to describe how likely an event is to occur, possibility theory uses two concepts, the possibility and the necessity of the event. For any set
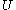, the necessity measure is defined by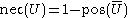In the above formula,
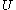denotes the complement of , that is the elements of 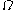that do not belong to . It is straightforward to show that: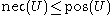 for any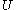 and that:
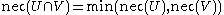
Note that contrary to probability theory, possibility is not self-dual. That is, for any event
, we only have the inequality: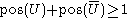However, the following duality rule holds:
- For any event
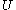, either 
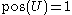, or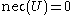 
Accordingly, beliefs about an event can be represented by a number and a bit.
Interpretation
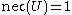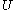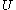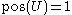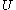There are four cases that can be interpreted as follows: means that is necessary. is certainly true. It implies that . means that is impossible. is certainly false. It implies that 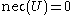. means that 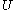is possible. I would not be surprised at all if 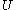occurs. It leaves 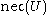unconstrained. means that is unnecessary. I would not be surprised at all if 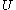does not occur. It leaves unconstrained.The intersection of the last two cases is
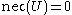and 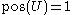meaning that I believe nothing at all about 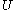. Because it allows for indeterminacy like this, possibility theory relates to the graduation of a many-valued logic, such as intuitionistic logicIntuitionistic logic
Intuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
, rather than the classical two-valued logic.
Note that unlike possibility, fuzzy logic is compositional with respect to both the union and the intersection operator. The relationship with fuzzy theory can be explained with the following classical example.
- Fuzzy logic: When a bottle is half full, it can be said that the level of truth of the proposition "The bottle is full" is 0.5. The word "full" is seen as a fuzzy predicate describing the amount of liquid in the bottle.
- Possibility theory: There is one bottle, either completely full or totally empty. The proposition "the possibility level that the bottle is full is 0.5" describes a degree of belief. One way to interpret 0.5 in that proposition is to define its meaning as: I am ready to bet that it's empty as long as the odds are even (1:1) or better, and I would not bet at any rate that it's full.
Possibility theory as an imprecise probability theory
There is an extensive formal correspondence between probability and possibility theories, where the addition operator corresponds to the maximum operator.A possibility measure can be seen as a consonant plausibility measure in Dempster–Shafer theory
Dempster-Shafer theory
The Dempster–Shafer theory is a mathematical theory of evidence. It allows one to combine evidence from different sources and arrive at a degree of belief that takes into account all the available evidence. The theory was first developed by Arthur P...
of evidence. The operators of possibility theory can be seen as a hyper-cautious version of the operators of the transferable belief model
Transferable belief model
The transferable belief model is an elaboration on the Dempster-Shafer theory of evidence.-Context:Consider the following classical problem of information fusion. A patient has an illness that can be caused by three different factors A, B and C...
, a modern development of the theory of evidence.
Possibility can be seen as an upper probability
Upper and lower probabilities
Upper and lower probabilities are representations of imprecise probability. Whereas probability theory uses a single number, the probability, to describe how likely an event is to occur, this method uses two numbers: the upper probability of the event and the lower probability of the event.Because...
: any possibility distribution defines a unique set of admissible probability distributions by
This allows one to study possibility theory using the tools of imprecise probabilities
Imprecise probability
Imprecise probability generalizes probability theory to allow for partial probability specifications, and is applicable when information is scarce, vague, or conflicting, in which case a unique probability distribution may be hard to identify...
.
Necessity logic
We call generalized possibility every function satisfying Axiom 1 and Axiom 3. We call generalized necessity the dual of a generalized possibility. The generalized necessities are related with a very simple and interesting fuzzy logic we call necessity logic. In the deduction apparatus of necessity logic the logical axioms are the usual classical tautologiesTautology (logic)
In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
. Also, there is only a fuzzy inference rule extending the usual Modus Ponens. Such a rule says that if α and α → β are proved at degree λ and μ, respectively, then we can assert β at degree min{λ,μ}. It is easy to see that the theories of such a logic are the generalized necessities and that the completely consistent theories coincide with the necessities (see for example Gerla 2001).
See also
- Logical possibilityLogical possibilityA logically possible proposition is one that can be asserted without implying a logical contradiction. This is to say that a proposition is logically possible if there is some coherent way for the world to be, under which the proposition would be true...
- Probability theoryProbability theoryProbability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
- Fuzzy measure theoryFuzzy measure theoryFuzzy measure theory considers a number of special classes of measures, each of which is characterized by a special property. Some of the measures used in this theory are plausibility and belief measures, fuzzy set membership function and the classical probability measures...
- Upper and lower probabilitiesUpper and lower probabilitiesUpper and lower probabilities are representations of imprecise probability. Whereas probability theory uses a single number, the probability, to describe how likely an event is to occur, this method uses two numbers: the upper probability of the event and the lower probability of the event.Because...
- Transferable belief modelTransferable belief modelThe transferable belief model is an elaboration on the Dempster-Shafer theory of evidence.-Context:Consider the following classical problem of information fusion. A patient has an illness that can be caused by three different factors A, B and C...