
Positive energy theorem
Encyclopedia
In general relativity
, the positive energy theorem (more commonly known as the positive mass conjecture in differential geometry) states that, assuming the dominant energy condition, the mass of an asymptotically flat spacetime
is non-negative; furthermore, the mass is zero only for Minkowski spacetime. The theorem is a scalar curvature
comparison theorem
, with asymptotic boundary conditions, and a corresponding statement of geometric rigidity.
The original proof of the theorem for ADM mass was provided by Richard Schoen
and Shing-Tung Yau
in 1979 using variational methods. Edward Witten
gave another proof in 1981 based on the use of spinor
s, inspired by positive energy theorems in the context of supergravity
. An extension of the theorem for the Bondi mass was given by Ludvigsen
and James Vickers, Gary Horowitz and Malcolm Perry
, and Schoen and Yau.
Gary Gibbons
, Stephen Hawking
, Horowitz and Perry proved extensions of the theorem to asymptotically anti-de Sitter spacetimes and to Einstein–Maxwell theory. The mass of an asymptotically anti-de Sitter spacetime is non-negative and only equal to zero for anti-de Sitter spacetime. In Einstein–Maxwell theory, for a spacetime with electric charge and magnetic charge
and magnetic charge 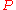 , the mass of the spacetime satisfies
, the mass of the spacetime satisfies

with equality for the Majumdar–Papapetrou extremal black hole
solutions.
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, the positive energy theorem (more commonly known as the positive mass conjecture in differential geometry) states that, assuming the dominant energy condition, the mass of an asymptotically flat spacetime
Asymptotically flat spacetime
An asymptotically flat spacetime is a Lorentzian manifold in which, roughly speaking, the curvature vanishes at large distances from some region, so that at large distances, the geometry becomes indistinguishable from that of Minkowski spacetime....
is non-negative; furthermore, the mass is zero only for Minkowski spacetime. The theorem is a scalar curvature
Scalar curvature
In Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
comparison theorem
Comparison theorem
A comparison theorem is any of a variety of theorems that compare properties of various mathematical objects.-Riemannian geometry:In Riemannian geometry it is a traditional name for a number of theorems that compare various metrics and provide various estimates in Riemannian geometry.*Rauch...
, with asymptotic boundary conditions, and a corresponding statement of geometric rigidity.
The original proof of the theorem for ADM mass was provided by Richard Schoen
Richard Schoen
Richard Melvin Schoen is an American mathematician. Born in Fort Recovery, Ohio, he received his PhD in 1977 from Stanford University where he is currently the Anne T. and Robert M. Bass Professor of Humanities and Sciences...
and Shing-Tung Yau
Shing-Tung Yau
Shing-Tung Yau is a Chinese American mathematician working in differential geometry. He was born in Shantou, Guangdong Province, China into a family of scholars from Jiaoling, Guangdong Province....
in 1979 using variational methods. Edward Witten
Edward Witten
Edward Witten is an American theoretical physicist with a focus on mathematical physics who is currently a professor of Mathematical Physics at the Institute for Advanced Study....
gave another proof in 1981 based on the use of spinor
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
s, inspired by positive energy theorems in the context of supergravity
Supergravity
In theoretical physics, supergravity is a field theory that combines the principles of supersymmetry and general relativity. Together, these imply that, in supergravity, the supersymmetry is a local symmetry...
. An extension of the theorem for the Bondi mass was given by Ludvigsen
Malcolm Ludvigsen
Malcolm Ludvigsen is an artist and scientist. He is an oil-painter with a particular interest in figure and en plein-air painting, and professor of mathematics with a special interest in relativity, black holes, the positive energy theorem and cosmology. He is the author of a book on general...
and James Vickers, Gary Horowitz and Malcolm Perry
Malcolm Perry (physicist)
Malcolm John Perry, is a theoretical physicist. Perry is a professor of theoretical physics at the University of Cambridge. His research mainly concerns general relativity, supergravity and string theory....
, and Schoen and Yau.
Gary Gibbons
Gary Gibbons
Gary William Gibbons , FRS, is a British theoretical physicist. Gibbons studied in Cambridge,where in 1969 he became a research student under the supervision of Dennis Sciama. When Sciama moved to Oxford, he became a student of Stephen Hawking, obtaining his PhD from Cambridge in 1973...
, Stephen Hawking
Stephen Hawking
Stephen William Hawking, CH, CBE, FRS, FRSA is an English theoretical physicist and cosmologist, whose scientific books and public appearances have made him an academic celebrity...
, Horowitz and Perry proved extensions of the theorem to asymptotically anti-de Sitter spacetimes and to Einstein–Maxwell theory. The mass of an asymptotically anti-de Sitter spacetime is non-negative and only equal to zero for anti-de Sitter spacetime. In Einstein–Maxwell theory, for a spacetime with electric charge
 and magnetic charge
and magnetic charge 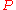 , the mass of the spacetime satisfies
, the mass of the spacetime satisfies
with equality for the Majumdar–Papapetrou extremal black hole
Extremal black hole
In theoretical physics, an extremal black hole is a black hole with the minimal possible mass that can be compatible with a given charge and angular momentum . In other words, this is the smallest possible black hole that can exist while rotating at a given fixed constant speed.The concept of an...
solutions.
See also
- In 1984 Schoen used the positive mass theorem in his work which completed the solution of the Yamabe problemYamabe problemThe Yamabe problem in differential geometry concerns the existence of Riemannian metrics with constant scalar curvature, and takes its name from the mathematician Hidehiko Yamabe. Although claimed to have a solution in 1960, a critical error...
. - The positive mass theorem was used in Hubert Bray's proof of the Riemannian Penrose inequalityRiemannian Penrose inequalityIn mathematical general relativity, the Penrose inequality, first conjectured by Sir Roger Penrose, estimates the mass of a spacetime in terms of the total area of its black holes and is a generalization of the positive mass theorem. The Riemannian Penrose inequality is the most important special...
.

