
Positive and negative sets
Encyclopedia
In measure theory, given a measurable space
(X,Σ) and a signed measure
μ on it, a set A ∈ Σ is called a positive set for μ if every Σ-measurable subset of A has nonnegative measure; that is, for every E ⊆ A that satisfies E ∈ Σ, one has μ(E) ≥ 0.
Similarly, a set A ∈ Σ is called a negative set for μ if for every subset E of A satisfying E ∈ Σ, one has μ(E) ≤ 0.
Intuitively, a measurable set A is positive (resp. negative) for μ if μ is nonnegative (resp. nonpositive) everywhere on A. Of course, if μ is a nonnegative measure
, every element of Σ is a positive set for μ.
In the light of Radon–Nikodym theorem
, if ν is a σ-finite positive measure such that |μ| << ν, a set A is a positive set for μ if and only if
the Radon–Nikodym derivative dμ/dν is nonnegative ν-almost everywhere on A. Similarly, a negative set is a set where dμ/dν ≤ 0 ν-almost everywhere.
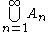
is also a positive set; the same is true if the word "positive" is replaced by "negative".
A set which is both positive and negative is a μ-null set
, for if E is a measurable subset of a positive and negative set A, then both μ(E) ≥ 0 and μ(E) ≤ 0 must hold, and therefore, μ(E) = 0.
states that for every measurable space (X,Σ) with a signed measure μ, there is a partition
of X into a positive and a negative set; such a partition (P,N) is unique up to
μ-null sets, and is called a Hahn decomposition of the signed measure μ.
Given a Hahn decomposition (P,N) of X, it is easy to show that A ⊆ X is a positive set if and only if A differs from a subset of P by a μ-null set; equivalently, if A−P is μ-null. The same is true for negative sets, if N is used instead of P.
Sigma-algebra
In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
(X,Σ) and a signed measure
Signed measure
In mathematics, signed measure is a generalization of the concept of measure by allowing it to have negative values. Some authors may call it a charge, by analogy with electric charge, which is a familiar distribution that takes on positive and negative values.-Definition:There are two slightly...
μ on it, a set A ∈ Σ is called a positive set for μ if every Σ-measurable subset of A has nonnegative measure; that is, for every E ⊆ A that satisfies E ∈ Σ, one has μ(E) ≥ 0.
Similarly, a set A ∈ Σ is called a negative set for μ if for every subset E of A satisfying E ∈ Σ, one has μ(E) ≤ 0.
Intuitively, a measurable set A is positive (resp. negative) for μ if μ is nonnegative (resp. nonpositive) everywhere on A. Of course, if μ is a nonnegative measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
, every element of Σ is a positive set for μ.
In the light of Radon–Nikodym theorem
Radon–Nikodym theorem
In mathematics, the Radon–Nikodym theorem is a result in measure theory that states that, given a measurable space , if a σ-finite measure ν on is absolutely continuous with respect to a σ-finite measure μ on , then there is a measurable function f on X and taking values in [0,∞), such that\nu =...
, if ν is a σ-finite positive measure such that |μ| << ν, a set A is a positive set for μ if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the Radon–Nikodym derivative dμ/dν is nonnegative ν-almost everywhere on A. Similarly, a negative set is a set where dμ/dν ≤ 0 ν-almost everywhere.
Properties
It follows from the definition that every measurable subset of a positive or negative set is also positive or negative. Also, the union of a sequence of positive or negative sets is also positive or negative; more formally, if (An)n is a sequence of positive sets, then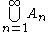
is also a positive set; the same is true if the word "positive" is replaced by "negative".
A set which is both positive and negative is a μ-null set
Null set
In mathematics, a null set is a set that is negligible in some sense. For different applications, the meaning of "negligible" varies. In measure theory, any set of measure 0 is called a null set...
, for if E is a measurable subset of a positive and negative set A, then both μ(E) ≥ 0 and μ(E) ≤ 0 must hold, and therefore, μ(E) = 0.
Hahn decomposition
The Hahn decomposition theoremHahn decomposition theorem
In mathematics, the Hahn decomposition theorem, named after the Austrian mathematician Hans Hahn, states that given a measurable space and a signed measure μ defined on the σ-algebra Σ, there exist two sets P and N in Σ such that:...
states that for every measurable space (X,Σ) with a signed measure μ, there is a partition
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of X into a positive and a negative set; such a partition (P,N) is unique up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
μ-null sets, and is called a Hahn decomposition of the signed measure μ.
Given a Hahn decomposition (P,N) of X, it is easy to show that A ⊆ X is a positive set if and only if A differs from a subset of P by a μ-null set; equivalently, if A−P is μ-null. The same is true for negative sets, if N is used instead of P.

