Positive and negative parts
Encyclopedia
In mathematics
, the positive part of a real
or extended real
-valued function
is defined by the formula
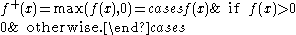
Intuitively, the graph
of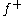
is obtained by taking the graph of 
, chopping off the part under the x-axis, and letting 
take the value zero there.
Similarly, the negative part of f is defined as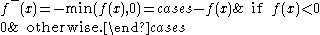
Note that both f+ and f− are non-negative functions. A peculiarity of terminology is that the 'negative part' is neither negative nor a part (like the imaginary part of a complex number
is neither imaginary nor a part).
The function f can be expressed in terms of f+ and f− as
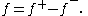
Also note that
.
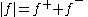Using these two equations one may express the positive and negative parts as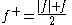
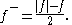
Another representation, using the Iverson bracket is
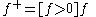
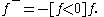
One may define the positive and negative part of any function with values in a linearly ordered group
.
(X,Σ), an extended real-valued function f is measurable
if and only if
its positive and negative parts are. Therefore, if such a function f is measurable, so is its absolute value |f|, being the sum of two measurable functions. The converse, though, does not necessarily hold: for example, taking f as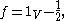
where V is a Vitali set
, it is clear that f is not measurable, but its absolute value is, being a constant function.
The positive part and negative part of a function are used to define the Lebesgue integral for a real-valued function. Analogously to this decomposition of a function, one may decompose a signed measure
into positive and negative parts — see the Hahn decomposition theorem
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the positive part of a real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or extended real
Extended real number line
In mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...
-valued function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
is defined by the formula
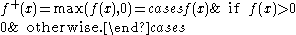
Intuitively, the graph
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
of
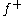is obtained by taking the graph of , chopping off the part under the x-axis, and letting take the value zero there.Similarly, the negative part of f is defined as
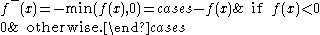
Note that both f+ and f− are non-negative functions. A peculiarity of terminology is that the 'negative part' is neither negative nor a part (like the imaginary part of a complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
is neither imaginary nor a part).
The function f can be expressed in terms of f+ and f− as
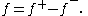
Also note that
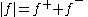.Using these two equations one may express the positive and negative parts as
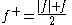
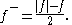
Another representation, using the Iverson bracket is
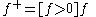
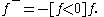
One may define the positive and negative part of any function with values in a linearly ordered group
Linearly ordered group
In abstract algebra a linearly ordered or totally ordered group is an ordered group G such that the order relation "≤" is total...
.
Measure-theoretic properties
Given a measurable spaceSigma-algebra
In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
(X,Σ), an extended real-valued function f is measurable
Measurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
its positive and negative parts are. Therefore, if such a function f is measurable, so is its absolute value |f|, being the sum of two measurable functions. The converse, though, does not necessarily hold: for example, taking f as
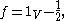
where V is a Vitali set
Vitali set
In mathematics, a Vitali set is an elementary example of a set of real numbers that is not Lebesgue measurable, found by . The Vitali theorem is the existence theorem that there are such sets. There are uncountably many Vitali sets, and their existence is proven on the assumption of the axiom of...
, it is clear that f is not measurable, but its absolute value is, being a constant function.
The positive part and negative part of a function are used to define the Lebesgue integral for a real-valued function. Analogously to this decomposition of a function, one may decompose a signed measure
Signed measure
In mathematics, signed measure is a generalization of the concept of measure by allowing it to have negative values. Some authors may call it a charge, by analogy with electric charge, which is a familiar distribution that takes on positive and negative values.-Definition:There are two slightly...
into positive and negative parts — see the Hahn decomposition theorem
Hahn decomposition theorem
In mathematics, the Hahn decomposition theorem, named after the Austrian mathematician Hans Hahn, states that given a measurable space and a signed measure μ defined on the σ-algebra Σ, there exist two sets P and N in Σ such that:...
.
External links
- Positive part on MathWorldMathWorldMathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...