
Porous set
Encyclopedia
In mathematics
, a porosity is a concept in the study of metric space
s. Like the concepts of meagre
and measure zero sets, porosity is a notion of a set being somehow "sparse" or "lacking bulk"; however, porosity is not equivalent to either of the above notions, as shown below.
metric space and let E be a subset of X. Let B(x, r) denote the closed ball in (X, d) with centre x ∈ X and radius r > 0. E is said to be porous if there exist constants 0 < α < 1 and r0 > 0 such that, for every 0 < r ≤ r0 and every x ∈ X, there is some point y ∈ X with
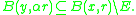
A subset of X is called σ-porous if it is a countable
union
of porous subsets of X.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a porosity is a concept in the study of metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s. Like the concepts of meagre
Meagre set
In the mathematical fields of general topology and descriptive set theory, a meagre set is a set that, considered as a subset of a topological space, is in a precise sense small or negligible...
and measure zero sets, porosity is a notion of a set being somehow "sparse" or "lacking bulk"; however, porosity is not equivalent to either of the above notions, as shown below.
Definition
Let (X, d) be a completeComplete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
metric space and let E be a subset of X. Let B(x, r) denote the closed ball in (X, d) with centre x ∈ X and radius r > 0. E is said to be porous if there exist constants 0 < α < 1 and r0 > 0 such that, for every 0 < r ≤ r0 and every x ∈ X, there is some point y ∈ X with
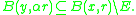
A subset of X is called σ-porous if it is a countable
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of porous subsets of X.
Properties
- Any porous set is nowhere dense. Hence, all σ-porous sets are meagre sets (or of the first category).
- If X is a finite-dimensional Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn, then porous subsets are sets of Lebesgue measureLebesgue measureIn measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
zero. - However, there does exist a non-σ-porous subset P of Rn which is of the first category and of Lebesgue measure zero. This is known as Zajíček's theorem.
- The relationship between porosity and being nowhere dense can be illustrated as follows: if E is nowhere dense, then for x ∈ X and r > 0, there is a point y ∈ X and s > 0 such that
- However, if E is also porous, then it is possible to take s = αr (at least for small enough r), where 0 < α < 1 is a constant that depends only on E.


