
Polyphase matrix
Encyclopedia
In signal processing
,
a polyphase matrix is a matrix whose elements are filter mask
s.
It represents a filter bank
as it is used
in sub-band coders alias discrete wavelet transform
s.
If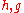 are two filters,
are two filters,
then one level the traditional wavelet transform
maps an input signal to two output signals
to two output signals 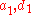 ,
,
each of the half length: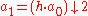
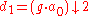
Note, that the dot means polynomial multiplication, i.e. convolution
and
 means downsampling
means downsampling
.
If the above formula is implemented directly, you will compute values
that are subsequently flushed by the down-sampling.
You can avoid that by splitting the filters and the signal
into even and odd indexed values before the transformation.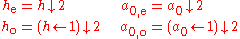
The arrows and
and 
denote left and right shifting, respectively.
They shall have the same precedence like convolution,
because they are in fact convolutions with a shifted discrete delta impulse.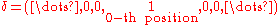
The wavelet transformation reformulated to the split filters is:

This can be written as matrix-vector-multiplication
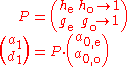
This matrix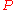 is the polyphase matrix.
is the polyphase matrix.
Of course, a polyphase matrix can have any size,
it need not to have square shape.
That is, the principle scales well to any filterbanks,
multiwavelets,
wavelet transforms based on fractional refinements.
is more than about write simplification.
It allows the adaptation of many results from matrix theory and module theory.
The following properties are explained for a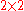 matrix,
matrix,
but they scale equally to higher dimensions.
is called perfect reconstruction property.
Mathematically this is equivalent to invertibility.
According to the theorem of invertibility
of a matrix over a ring,
the polyphase matrix is invertible if and only if
the determinant
of the polyphase matrix is a Kronecker delta,
which is zero everywhere except of one value.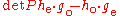

By Cramer's rule
the inverse of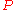
can be given immediately.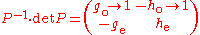
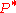
is also the inverse matrix of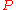 .
.
The adjoint matrix is the transposed matrix with adjoint filters.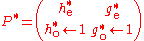
It implies, that the Euclidean norm of the input signals is preserved.
That is, the according wavelet transform is an isometry
.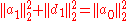
The orthogonality condition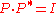
can be written out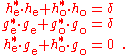
what Euclidean norms the output can assume.
This can be bounded by the help of the operator norm
.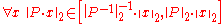
For the polyphase matrix
polyphase matrix
the Euclidean operator norm can be given explicitly
using the Frobenius norm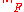 and the z transform
and the z transform  :
:
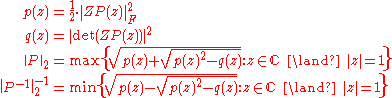
This is a special case of the matrix
matrix
where the operator norm can be obtained via z transform
and the spectral radius
of a matrix or the according spectral norm.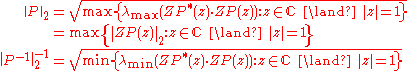
A signal, where these bounds are assumed
can be derived from the eigenvector
corresponding to the maximizing and minimizing eigenvalue.
.
For instance the decomposition into addition matrices
leads to the lifting scheme
.
However, classical matrix decompositions like LU
and QR decomposition
cannot be applied immediately,
because the filters form a ring with respect to convolution,
not a field.
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
,
a polyphase matrix is a matrix whose elements are filter mask
Linear filter
Linear filters in the time domain process time-varying input signals to produce output signals, subject to the constraint of linearity.This results from systems composed solely of components classified as having a linear response....
s.
It represents a filter bank
Filter bank
In signal processing, a filter bank is an array of band-pass filters that separates the input signal into multiple components, each one carrying a single frequency subband of the original signal. One application of a filter bank is a graphic equalizer, which can attenuate the components...
as it is used
in sub-band coders alias discrete wavelet transform
Discrete wavelet transform
In numerical analysis and functional analysis, a discrete wavelet transform is any wavelet transform for which the wavelets are discretely sampled...
s.
If
 are two filters,
are two filters,then one level the traditional wavelet transform
maps an input signal
 to two output signals
to two output signals 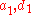 ,
,each of the half length:
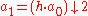
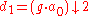
Note, that the dot means polynomial multiplication, i.e. convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
and
 means downsampling
means downsamplingDownsampling
In signal processing, downsampling is the process of reducing the sampling rate of a signal. This is usually done to reduce the data rate or the size of the data....
.
If the above formula is implemented directly, you will compute values
that are subsequently flushed by the down-sampling.
You can avoid that by splitting the filters and the signal
into even and odd indexed values before the transformation.
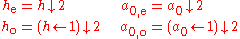
The arrows
 and
and 
denote left and right shifting, respectively.
They shall have the same precedence like convolution,
because they are in fact convolutions with a shifted discrete delta impulse.
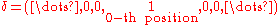
The wavelet transformation reformulated to the split filters is:


This can be written as matrix-vector-multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
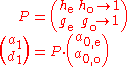
This matrix
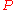 is the polyphase matrix.
is the polyphase matrix.Of course, a polyphase matrix can have any size,
it need not to have square shape.
That is, the principle scales well to any filterbanks,
multiwavelets,
wavelet transforms based on fractional refinements.
Properties
The representation of sub-band coding by the polyphase matrixis more than about write simplification.
It allows the adaptation of many results from matrix theory and module theory.
The following properties are explained for a
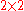 matrix,
matrix,but they scale equally to higher dimensions.
Invertibility / Perfect reconstruction
The case that a polyphase matrix allows reconstruction of a processed signal from the filtered data,is called perfect reconstruction property.
Mathematically this is equivalent to invertibility.
According to the theorem of invertibility
of a matrix over a ring,
the polyphase matrix is invertible if and only if
the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the polyphase matrix is a Kronecker delta,
which is zero everywhere except of one value.
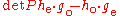

By Cramer's rule
Cramer's rule
In linear algebra, Cramer's rule is a theorem, which gives an expression for the solution of a system of linear equations with as many equations as unknowns, valid in those cases where there is a unique solution...
the inverse of
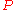
can be given immediately.
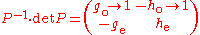
Orthogonality
Orthogonality means that the adjoint matrix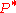
is also the inverse matrix of
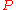 .
.The adjoint matrix is the transposed matrix with adjoint filters.
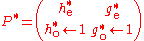
It implies, that the Euclidean norm of the input signals is preserved.
That is, the according wavelet transform is an isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
.
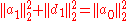
The orthogonality condition
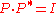
can be written out
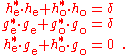
Operator norm
For non-orthogonal polyphase matrices the question ariseswhat Euclidean norms the output can assume.
This can be bounded by the help of the operator norm
Operator norm
In mathematics, the operator norm is a means to measure the "size" of certain linear operators. Formally, it is a norm defined on the space of bounded linear operators between two given normed vector spaces.- Introduction and definition :...
.
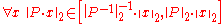
For the
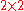 polyphase matrix
polyphase matrixthe Euclidean operator norm can be given explicitly
using the Frobenius norm
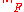 and the z transform
and the z transform  :
: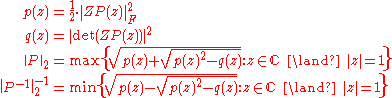
This is a special case of the
 matrix
matrixwhere the operator norm can be obtained via z transform
and the spectral radius
Spectral radius
In mathematics, the spectral radius of a square matrix or a bounded linear operator is the supremum among the absolute values of the elements in its spectrum, which is sometimes denoted by ρ.-Matrices:...
of a matrix or the according spectral norm.
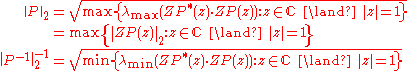
A signal, where these bounds are assumed
can be derived from the eigenvector
corresponding to the maximizing and minimizing eigenvalue.
Lifting scheme
The concept of the polyphase matrix allows matrix decompositionMatrix decomposition
In the mathematical discipline of linear algebra, a matrix decomposition is a factorization of a matrix into some canonical form. There are many different matrix decompositions; each finds use among a particular class of problems.- Example :...
.
For instance the decomposition into addition matrices
Triangular matrix
In the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
leads to the lifting scheme
Lifting scheme
The lifting scheme is a technique for both designing wavelets and performing the discrete wavelet transform.Actually it is worthwhile to merge these steps and design the wavelet filters while performing the wavelet transform....
.
However, classical matrix decompositions like LU
LU decomposition
In linear algebra, LU decomposition is a matrix decomposition which writes a matrix as the product of a lower triangular matrix and an upper triangular matrix. The product sometimes includes a permutation matrix as well. This decomposition is used in numerical analysis to solve systems of linear...
and QR decomposition
QR decomposition
In linear algebra, a QR decomposition of a matrix is a decomposition of a matrix A into a product A=QR of an orthogonal matrix Q and an upper triangular matrix R...
cannot be applied immediately,
because the filters form a ring with respect to convolution,
not a field.

