
Polyhedral space
Encyclopedia
In mathematics
, specifically in metric geometry, a polyhedral space is a certain metric space. A (Euclidean
) polyhedral space is a (usually finite) simplicial complex
in which every simplex has a flat
metric. (Other spaces of interest are spherical and hypebolic polyhedral spaces, where every simplex has a metric of constant positive or negative curvature). In the sequel all polyhedral spaces are taken to be Euclidean polyhedral spaces.
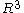 is a 2-dimensional polyhedral space.
is a 2-dimensional polyhedral space.
Any PL-manifold (which is essentially the same as a simplicial manifold
, just with some technical assumptions for convenience) is an example of a polyhedral space. In fact, one can consider pseudomanifolds, although it makes more sense to restrict the attention to normal pseudomanifolds.
s) metric singularities play a central role. Let a polyhedral space be an n-dimensional manifold. If a point in a polyhedral space that is an n-dimensional topological manifold has no neighborhood isometric to a Euclidean neighborhood in R^n, this point is said to be a metric singularity. It is a singularity of codimension k, if it has a neighborhood isometric to R^{n-k} with a metric cone. Singularities of codimension 2 are of major importance; they are characterized by a single number, the conical angle.
The singularities can also studied topologically. Then, for example, there are no topological singularities of codimension 2. In a 3-dimensional polyhedral space without a boundary (faces not glued to other faces) any point has a neighborhood homeomorphic either to an open ball or to a cone over the projective plane
. In the former case, the point is necessarily a codimension 3 metric singularity. The general problem of topologically classifying singularities in polyhedral spaces is largely unresolved (apart from simple statements that e.g. any singularity is locally a cone over a spherical polyhedral space one dimension less and we can study singularities there).
), specifically polyhedral spaces of nonnegative and nonpositive curvature. Nonnegative curvature on singularities of codimension 2 implies nonnegative curvature overall. However, this is false for nonpositive curvature. For example, consider R^3 with one octant removed. Then on the edges of this octant (singularities of codimension 2) the curvature is nonpositive (because of branching geodesics), yet it is not the case at the origin (singularity of codimension 3), where a triangle such as (0,0,e), (0,e,0), (e,0,0) has a median longer than would be in the Euclidean plane, which is characteristic of nonnegative curvature.
can be applied. There is only one obvious notion of parallel transport
and only one natural connection
. The concept of holonomy
is strikingly simple in this case. The restricted holonomy group is trivial, and so there is a homomorphism
from the fundamental group
onto the holonomy group. It may be especially convenient to remove all singularities to obtain a space with a flat Riemannian metric and to study the holonomies there. One concepts thus arising are polyhedral Kähler manifolds, when the holonomies are contained in a group, conjugate to the unitary matrices. In this case, the holonomies also preserve a symplectic form, together with a complex structure on this polyhedral space (manifold) with the singularities removed.
All the concepts such as differential form
, L2 differential form, etc. are adjusted accordingly.
in polyhedral spaces, e.g. of nonpositive curvature (hyperbolic billiards). Positively curved polyhedral spaces arise also as links of points (typically metric singularities) in Euclidean polyhedral spaces.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in metric geometry, a polyhedral space is a certain metric space. A (Euclidean
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
) polyhedral space is a (usually finite) simplicial complex
Simplicial complex
In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
in which every simplex has a flat
Flat
In music, flat, or Bemolle , means "lower in pitch"; the flat symbol lowers a note by a half step. Intonation may be flat, sharp, or both, successively or simultaneously...
metric. (Other spaces of interest are spherical and hypebolic polyhedral spaces, where every simplex has a metric of constant positive or negative curvature). In the sequel all polyhedral spaces are taken to be Euclidean polyhedral spaces.
Examples
All 1-dimensional polyhedral spaces are just metric graphs. A good source of 2-dimensional examples constitute triangulations of 2-dimensional surfaces. The surface of a convex polyhedron in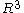 is a 2-dimensional polyhedral space.
is a 2-dimensional polyhedral space.Any PL-manifold (which is essentially the same as a simplicial manifold
Simplicial manifold
In mathematics, the term simplicial manifold commonly refers to either of two different types of objects, which combine attributes of a simplex with those of a manifold. Briefly; a simplex is a generalization of the concept of a triangle into forms with more, or fewer, than two dimensions. ...
, just with some technical assumptions for convenience) is an example of a polyhedral space. In fact, one can consider pseudomanifolds, although it makes more sense to restrict the attention to normal pseudomanifolds.
Metric singularities
In the study of polyhedral spaces (particularly of those that are also topological manifoldTopological manifold
In mathematics, a topological manifold is a topological space which looks locally like Euclidean space in a sense defined below...
s) metric singularities play a central role. Let a polyhedral space be an n-dimensional manifold. If a point in a polyhedral space that is an n-dimensional topological manifold has no neighborhood isometric to a Euclidean neighborhood in R^n, this point is said to be a metric singularity. It is a singularity of codimension k, if it has a neighborhood isometric to R^{n-k} with a metric cone. Singularities of codimension 2 are of major importance; they are characterized by a single number, the conical angle.
The singularities can also studied topologically. Then, for example, there are no topological singularities of codimension 2. In a 3-dimensional polyhedral space without a boundary (faces not glued to other faces) any point has a neighborhood homeomorphic either to an open ball or to a cone over the projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
. In the former case, the point is necessarily a codimension 3 metric singularity. The general problem of topologically classifying singularities in polyhedral spaces is largely unresolved (apart from simple statements that e.g. any singularity is locally a cone over a spherical polyhedral space one dimension less and we can study singularities there).
Curvature
It is interesting to study the curvature of polyhedral spaces (the curvature in the sense of Alexandrov spacesAlexandrov topology
In topology, an Alexandrov space is a topological space in which the intersection of any family of open sets is open. It is an axiom of topology that the intersection of any finite family of open sets is open...
), specifically polyhedral spaces of nonnegative and nonpositive curvature. Nonnegative curvature on singularities of codimension 2 implies nonnegative curvature overall. However, this is false for nonpositive curvature. For example, consider R^3 with one octant removed. Then on the edges of this octant (singularities of codimension 2) the curvature is nonpositive (because of branching geodesics), yet it is not the case at the origin (singularity of codimension 3), where a triangle such as (0,0,e), (0,e,0), (e,0,0) has a median longer than would be in the Euclidean plane, which is characteristic of nonnegative curvature.
Additional structure
Many concepts of Riemannian geometryRiemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
can be applied. There is only one obvious notion of parallel transport
Parallel transport
In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...
and only one natural connection
Connection (mathematics)
In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
. The concept of holonomy
Holonomy
In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...
is strikingly simple in this case. The restricted holonomy group is trivial, and so there is a homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
from the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
onto the holonomy group. It may be especially convenient to remove all singularities to obtain a space with a flat Riemannian metric and to study the holonomies there. One concepts thus arising are polyhedral Kähler manifolds, when the holonomies are contained in a group, conjugate to the unitary matrices. In this case, the holonomies also preserve a symplectic form, together with a complex structure on this polyhedral space (manifold) with the singularities removed.
All the concepts such as differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
, L2 differential form, etc. are adjusted accordingly.
Other topics
Another direction of research are developments of billiardsBilliards
Cue sports , also known as billiard sports, are a wide variety of games of skill generally played with a cue stick which is used to strike billiard balls, moving them around a cloth-covered billiards table bounded by rubber .Historically, the umbrella term was billiards...
in polyhedral spaces, e.g. of nonpositive curvature (hyperbolic billiards). Positively curved polyhedral spaces arise also as links of points (typically metric singularities) in Euclidean polyhedral spaces.

