
Polyconvex function
Encyclopedia
In mathematics
, the notion of polyconvexity is a generalization of the notion of convexity
for functions
defined on spaces of matrices
. Let Mm×n(K) denote the space of all m × n matrices over the field K, which may be either the real number
s R, or the complex number
s C. A function f : Mm×n(K) → R ∪ {±∞} is said to be polyconvex if
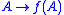
can be written as a convex function of the p × p subdeterminant
s of A, for 1 ≤ p ≤ min{m, n}.
Polyconvexity is a weaker property than convexity. For example, the function f given by
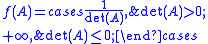
is polyconvex but not convex.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the notion of polyconvexity is a generalization of the notion of convexity
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
for functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
defined on spaces of matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. Let Mm×n(K) denote the space of all m × n matrices over the field K, which may be either the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s R, or the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s C. A function f : Mm×n(K) → R ∪ {±∞} is said to be polyconvex if
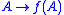
can be written as a convex function of the p × p subdeterminant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
s of A, for 1 ≤ p ≤ min{m, n}.
Polyconvexity is a weaker property than convexity. For example, the function f given by
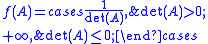
is polyconvex but not convex.

