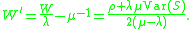Pollaczek-Khinchine formula
Encyclopedia
In queueing theory
, a discipline within the mathematical theory of probability
, the Pollaczek–Khinchine formula is a formula for the mean queue length in a model where jobs arrive according to a Poisson process
and service times have a general distribution (an M/G/1 queue
). It can also be used to calculate the mean waiting time in such a model.
The formula was first published by Felix Pollaczek
and recast in probabilistic terms by Aleksandr Khinchin two years later.
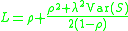
where
For the mean queue length to be finite it is necessary that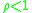 as otherwise jobs arrive faster than they leave the queue. "Traffic intensity," ranges between 0 and 1, and is the mean fraction of time that the server is busy. If the arrival rate
as otherwise jobs arrive faster than they leave the queue. "Traffic intensity," ranges between 0 and 1, and is the mean fraction of time that the server is busy. If the arrival rate  is greater than or equal to the service rate
is greater than or equal to the service rate  , the queuing delay becomes infinite. The variance term enters the expression due to Feller's paradox
, the queuing delay becomes infinite. The variance term enters the expression due to Feller's paradox
.
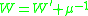 where
where  is the mean waiting time (time spent in the queue waiting for service) and
is the mean waiting time (time spent in the queue waiting for service) and 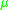 is the service rate. Using Little's law
is the service rate. Using Little's law
, which states that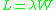
where
so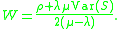
We can write an expression for the mean waiting time as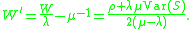
Queueing theory
Queueing theory is the mathematical study of waiting lines, or queues. The theory enables mathematical analysis of several related processes, including arriving at the queue, waiting in the queue , and being served at the front of the queue...
, a discipline within the mathematical theory of probability
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, the Pollaczek–Khinchine formula is a formula for the mean queue length in a model where jobs arrive according to a Poisson process
Poisson process
A Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
and service times have a general distribution (an M/G/1 queue
M/G/1 queue
In queueing theory, a discipline within the mathematical theory of probability, a M/G/1 queue represents the queue length in a system having a single server, where arrivals are detemined by a Poisson process and job service times can have an arbitrary distribution...
). It can also be used to calculate the mean waiting time in such a model.
The formula was first published by Felix Pollaczek
Felix Pollaczek
Félix Pollaczek was an Austrian-French engineer and mathematician, known for numerous contributions to number theory, mathematical analysis, mathematical physics and probability theory...
and recast in probabilistic terms by Aleksandr Khinchin two years later.
Mean queue length
The formula states that the mean queue length L is given by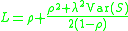
where
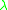 is the arrival rate of the Poisson processPoisson processA Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
is the arrival rate of the Poisson processPoisson processA Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...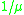 is the mean of the service time distribution S
is the mean of the service time distribution S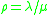 is the utilizationUtilizationUtilization is a statistical concept as well as a primary business measure for the rental industry.-Queueing theory:In queueing theory, utilization is the proportion of the system's resources which is used by the traffic which arrives at it. It should be strictly less than one for the system to...
is the utilizationUtilizationUtilization is a statistical concept as well as a primary business measure for the rental industry.-Queueing theory:In queueing theory, utilization is the proportion of the system's resources which is used by the traffic which arrives at it. It should be strictly less than one for the system to...- Var(S) is the varianceVarianceIn probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of the service time distribution S.
For the mean queue length to be finite it is necessary that
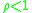 as otherwise jobs arrive faster than they leave the queue. "Traffic intensity," ranges between 0 and 1, and is the mean fraction of time that the server is busy. If the arrival rate
as otherwise jobs arrive faster than they leave the queue. "Traffic intensity," ranges between 0 and 1, and is the mean fraction of time that the server is busy. If the arrival rate  is greater than or equal to the service rate
is greater than or equal to the service rate  , the queuing delay becomes infinite. The variance term enters the expression due to Feller's paradox
, the queuing delay becomes infinite. The variance term enters the expression due to Feller's paradoxPalm calculus
In the study of stochastic processes, Palm calculus, named after Swedish teletrafficist Conny Palm, is the study of the relationship between probabilities conditioned on a specified event and time average probabilities...
.
Mean waiting time
If we write W for the mean time a customer spends in the queue, then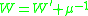 where
where  is the mean waiting time (time spent in the queue waiting for service) and
is the mean waiting time (time spent in the queue waiting for service) and 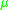 is the service rate. Using Little's law
is the service rate. Using Little's lawLittle's law
In the mathematical theory of queues, Little's result, theorem, lemma, law or formula says:It is a restatement of the Erlang formula, based on the work of Danish mathematician Agner Krarup Erlang...
, which states that
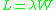
where
- L is the mean queue length
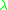 is the arrival rate of the Poisson processPoisson processA Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
is the arrival rate of the Poisson processPoisson processA Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...- W is the mean time spent at the queue both waiting and being serviced,
so
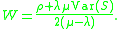
We can write an expression for the mean waiting time as