
Palm calculus
Encyclopedia
In the study of stochastic process
es, Palm calculus, named after Swedish teletrafficist
Conny Palm
, is the study of the relationship between probabilities
conditioned on a specified event and time average probabilities. A Palm probability or Palm expectation
, often denoted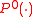 or
or 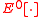 , is a probability or expectation conditioned on a specified event occurring at time 0.
, is a probability or expectation conditioned on a specified event occurring at time 0.
 , which states that the time-average number of users (L) in a system is equal to the product of the rate (
, which states that the time-average number of users (L) in a system is equal to the product of the rate ( ) at which users arrive and the Palm-average waiting time (W) that a user spends in the system. That is, the average W gives equal weight to the waiting time of all customers, rather than being the time average of "the waiting times of the customers currently in the system".
) at which users arrive and the Palm-average waiting time (W) that a user spends in the system. That is, the average W gives equal weight to the waiting time of all customers, rather than being the time average of "the waiting times of the customers currently in the system".
is greater than the expected interval between points. The latter is the Palm expectation of the former, conditioning on the event that a point occurs at the time of the observation. This paradox occurs because large intervals are given greater weight in the time average than small intervals.
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
es, Palm calculus, named after Swedish teletrafficist
Teletraffic engineering
Telecommunications traffic engineering, teletraffic engineering, or traffic engineering is the application of traffic engineering theory to telecommunications...
Conny Palm
Conny Palm
Conrad "Conny" Palm was a Swedish electrical engineer and statistician, known for several contributions to teletraffic engineering and queueing theory....
, is the study of the relationship between probabilities
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
conditioned on a specified event and time average probabilities. A Palm probability or Palm expectation
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
, often denoted
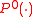 or
or 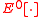 , is a probability or expectation conditioned on a specified event occurring at time 0.
, is a probability or expectation conditioned on a specified event occurring at time 0.Little's formula
A simple example of a formula from Palm calculus is Little's lawLittle's law
In the mathematical theory of queues, Little's result, theorem, lemma, law or formula says:It is a restatement of the Erlang formula, based on the work of Danish mathematician Agner Krarup Erlang...
 , which states that the time-average number of users (L) in a system is equal to the product of the rate (
, which states that the time-average number of users (L) in a system is equal to the product of the rate ( ) at which users arrive and the Palm-average waiting time (W) that a user spends in the system. That is, the average W gives equal weight to the waiting time of all customers, rather than being the time average of "the waiting times of the customers currently in the system".
) at which users arrive and the Palm-average waiting time (W) that a user spends in the system. That is, the average W gives equal weight to the waiting time of all customers, rather than being the time average of "the waiting times of the customers currently in the system".Feller's paradox
An important example of the use of Palm probabilities is Feller's paradox, often associated with the analysis of an M/G/1 queue. This states that the (time-)average time between the previous and next points in a point processPoint process
In statistics and probability theory, a point process is a type of random process for which any one realisation consists of a set of isolated points either in time or geographical space, or in even more general spaces...
is greater than the expected interval between points. The latter is the Palm expectation of the former, conditioning on the event that a point occurs at the time of the observation. This paradox occurs because large intervals are given greater weight in the time average than small intervals.

