Peres-Horodecki criterion
Encyclopedia
The Peres-Horodecki criterion is a necessary condition, for the joint density matrix
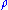of two quantum mechanical systems 
and 
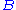, to be separable
. It is also called the PPT criterion, for positive partial transpose. In the 2x2 and 2x3 dimensional cases the condition is also sufficient. It is used to decide the separability of mixed states, where the Schmidt decomposition does not apply.
In higher dimensions, the test is inconclusive, and one should supplement it with more advanced tests, such as those based on entanglement witness
es.
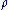which acts on 
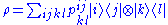
Its partial transpose
(with respect to the B party) is defined as
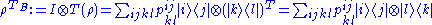
Note that the partial in the name implies that only part of the state is transposed. More precisely,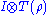
is the identity map applied to the A party and the transposition map applied to the B party.
This definition can be seen more clearly if we write the state as a block matrix:
Where
, and each block is a square matrix of dimension 
. Then the partial transpose is
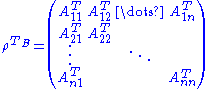
The criterion states that if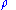
is separable, 
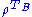has non-negative eigenvalues. In other words, if 
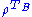has a negative eigenvalue, 
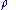is guaranteed to be entangled
. If the eigenvalues are non-negative, and the dimension is larger than 6, the test is inconclusive.
The result is independent of the party that was transposed, because
.
s:
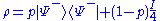
It can regarded as the convex combination
of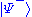
, a maximally entangled state, and identity, the maximally mixed state.
Its density matrix is
and the partial transpose
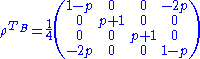
Its least eigenvalue is
. Therefore, the state is entangled for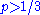 
.
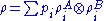
In this case, the effect of the partial transposition is trivial:
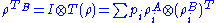
As the transposition map preserves eigenvalues, the spectrum of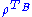
is the same as the spectrum of 
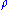, and in particular 
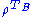must still be positive semidefinite. This proves the necessity of the PPT criterion.
Showing that being PPT is also sufficient for the 2 X 2 and 3 X 2 (equivalently 2 X 3) cases is more involved. It was shown by the Horodeckis that for every entangled state there exists an entanglement witness
. This is a result of geometric nature and invokes the Hahn–Banach theorem
(see reference below).
From the existence of entanglement witnesses, one can show that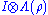
being positive for all positive maps
Λ is a necessary and sufficient condition for the separability of ρ, where Λ maps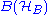
to 
Furthermore, every positive map from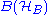
to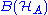 
can be decomposed into a sum of completely positive and completely copositive maps, when 
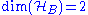and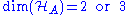 
. In other words, every such map Λ can be written as
where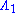
and 
are completely positive and T is the transposition map. This follows from the Størmer-Woronowicz theorem.
Loosely speaking, the transposition map is therefore the only one that can generate negative eigenvalues in these dimensions. So if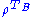
is positive, 
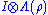is positive for any Λ. Thus we conclude that the Peres-Horodecki criterion is also sufficient for separability when 
.
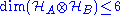In higher dimensions, however, there exists maps that can't be decomposed in this fashion, and the criterion is no longer sufficient. Consequently, there are entangled states which have a positive partial transpose. Such states have the interesting property that they are bound entangled, i.e. they can not be distilled
for quantum communication purposes.
Density matrix
In quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
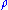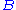of two quantum mechanical systems and , to be separableSeparable states
In quantum mechanics, separable quantum states are states without quantum entanglement.- Separable pure states :For simplicity, the following assumes all relevant state spaces are finite dimensional...
. It is also called the PPT criterion, for positive partial transpose. In the 2x2 and 2x3 dimensional cases the condition is also sufficient. It is used to decide the separability of mixed states, where the Schmidt decomposition does not apply.
In higher dimensions, the test is inconclusive, and one should supplement it with more advanced tests, such as those based on entanglement witness
Entanglement witness
In quantum information theory, an entanglement witness is an object of geometric nature which distinguishes an entangled state from separable ones.- Details :...
es.
Definition
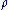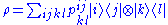
If we have a general state which acts on Its partial transpose
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
(with respect to the B party) is defined as
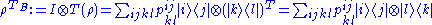
Note that the partial in the name implies that only part of the state is transposed. More precisely,
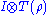is the identity map applied to the A party and the transposition map applied to the B party.This definition can be seen more clearly if we write the state as a block matrix:
Where
, and each block is a square matrix of dimension . Then the partial transpose is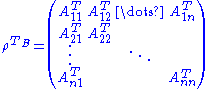The criterion states that if
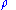is separable, 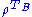has non-negative eigenvalues. In other words, if 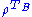has a negative eigenvalue, 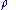is guaranteed to be entangledQuantum entanglement
Quantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
. If the eigenvalues are non-negative, and the dimension is larger than 6, the test is inconclusive.
The result is independent of the party that was transposed, because
.Example
Consider this 2-qubit family of Werner stateWerner state
A Werner state is a -dimensional bipartite quantum state that is invariant under all unitary operators of the form U \otimes U. That is, it is a quantum state ρ that satisfies\rho = \rho...
s:
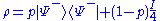
It can regarded as the convex combination
Convex combination
In convex geometry, a convex combination is a linear combination of points where all coefficients are non-negative and sum up to 1....
of
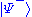, a maximally entangled state, and identity, the maximally mixed state.Its density matrix is
and the partial transpose
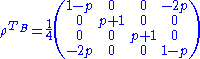
Its least eigenvalue is
. Therefore, the state is entangled for 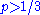.Demonstration
If ρ is separable, it can be written as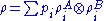In this case, the effect of the partial transposition is trivial:
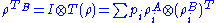
As the transposition map preserves eigenvalues, the spectrum of
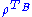is the same as the spectrum of 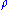, and in particular 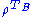must still be positive semidefinite. This proves the necessity of the PPT criterion.Showing that being PPT is also sufficient for the 2 X 2 and 3 X 2 (equivalently 2 X 3) cases is more involved. It was shown by the Horodeckis that for every entangled state there exists an entanglement witness
Entanglement witness
In quantum information theory, an entanglement witness is an object of geometric nature which distinguishes an entangled state from separable ones.- Details :...
. This is a result of geometric nature and invokes the Hahn–Banach theorem
Hahn–Banach theorem
In mathematics, the Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed...
(see reference below).
From the existence of entanglement witnesses, one can show that
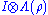being positive for all positive mapsChoi's theorem on completely positive maps
In mathematics, Choi's theorem on completely positive maps is a result that classifies completely positive maps between finite-dimensional C*-algebras...
Λ is a necessary and sufficient condition for the separability of ρ, where Λ maps
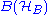to Furthermore, every positive map from
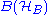to 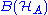can be decomposed into a sum of completely positive and completely copositive maps, when 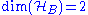and 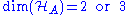. In other words, every such map Λ can be written aswhere
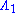and are completely positive and T is the transposition map. This follows from the Størmer-Woronowicz theorem.Loosely speaking, the transposition map is therefore the only one that can generate negative eigenvalues in these dimensions. So if
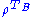is positive, 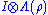is positive for any Λ. Thus we conclude that the Peres-Horodecki criterion is also sufficient for separability when 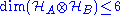.In higher dimensions, however, there exists maps that can't be decomposed in this fashion, and the criterion is no longer sufficient. Consequently, there are entangled states which have a positive partial transpose. Such states have the interesting property that they are bound entangled, i.e. they can not be distilled
Entanglement distillation
Entanglement distillation is the transformation of N copies of an arbitrary entangled state \rho into some number of approximately pure Bell pairs, using only local operations and classical communication...
for quantum communication purposes.