Parrondo's paradox
Encyclopedia
Parrondo's paradox, a paradox
in game theory
, has been described as: A losing strategy that wins. It is named after its creator, Spanish
physicist
Juan Parrondo
, who discovered the paradox in 1996. A more explanatory description is:
Parrondo devised the paradox in connection with his analysis of the Brownian ratchet
, a thought experiment
about a machine that can purportedly extract energy from random heat motions popularized by physicist Richard Feynman
.
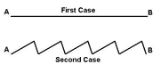
Consider an example in which there are two points A and B having the same altitude, as shown in Figure 1. In the first case, we have a flat profile connecting them. Here if we leave some round marbles in the middle that move back and forth in a random fashion, they will roll around randomly but towards both ends with an equal probability. Now consider the second case where we have a saw-tooth like region between them. Here also, the marbles will roll towards either ends with equal probability. Now if we tilt the whole profile towards the right, as shown in Figure 2, it is quite clear that both these cases will become biased towards B.
Now consider the game in which we alternate the two profiles while judiciously choosing the time between altering from one profile to the other in the following way.
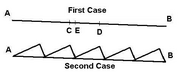When we leave a few marbles on the first profile at point E, they distribute themselves on the plane showing preferential movements towards point B. However, if we apply the second profile when some of the marbles have crossed the point C, but none have crossed point D, we will end up having most marbles back at point E (where we started from initially) but some also in the valley towards point A given sufficient time for the marbles to roll to the valley. Then we again apply the first profile and repeat the steps (points C, D and E now shifted one step to refer to the final valley closest to A). If no marbles cross point C before the first marble crosses point D, we must apply the second profile shortly before the first marble crosses point D, to start over.
It easily follows that eventually we will have marbles at point A, but none at point B. Hence for a problem defined with having marbles at point A being a win and having marbles at point B a loss, we clearly win by playing two losing games.
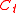to be our capital at time t, immediately before we play a game.
It is clear that by playing Game A, we will almost surely lose in the long run. Harmer and Abbott show via simulation that if
and 
Game B is an almost surely losing game as well. In fact, Game B is a Markov chain
, and an analysis of its state transition matrix (again with M=3) shows that the steady state probability of using coin 2 is 0.3836, and that of using coin 3 is 0.6164. As coin 2 is selected nearly 40% of the time, it has a disproportionate influence on the payoff from Game B, and results in it being a losing game.
However, when these two losing games are played in some alternating sequence - e.g. two games of A followed by two games of B (AABBAABB....), the combination of the two games is, paradoxically, a winning game. Not all alternating sequences of A and B result in winning games. For example, one game of A followed by one game of B (ABABAB...) is a losing game, while one game of A followed by two games of B (ABBABB....) is a winning game. This coin-tossing example has become the canonical illustration of Parrondo's paradox – two games, both losing when played individually, become a winning game when played in a particular alternating sequence. The apparent paradox has been explained using a number of sophisticated approaches, including Markov chains, flashing ratchets, Simulated Annealing and information theory. One way to explain the apparent paradox is as follows:
The role of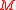
now comes into sharp focus. It serves solely to induce a dependence between Games A and B, so that a player is more likely to enter states in which Game B has a positive expectation, allowing it to overcome the losses from Game A. With this understanding, the paradox resolves itself: The individual games are losing only under a distribution that differs from that which is actually encountered when playing the compound game. In summary, Parrondo's paradox is an example of how dependence can wreak havoc with probabilistic computations made under a naive assumption of independence. A more detailed exposition of this point, along with several related examples, can be found in Philips and Feldman.
Parrondo's games are of little practical use such as for investing in stock market
s as the original games require the payoff from at least one of the interacting games to depend on the player's capital. However, the games need not be restricted to their original form and work continues in generalizing the phenomenon. Similarities to volatility pumping and the two-envelope problem
have been pointed out. Simple finance textbook models of security returns have been used to prove that individual investments with negative median long-term returns may be easily combined into diversified portfolios with positive median long-term returns. Similarly, a model that is often used to illustrate optimal betting rules has been used to prove that splitting bets between multiple games can turn a negative median long-term return into a positive one.
However, Derek Abbott
, a leading Parrondo's paradox researcher provides the following answer regarding the use of the word 'paradox' in this context:
Paradox
Similar to Circular reasoning, A paradox is a seemingly true statement or group of statements that lead to a contradiction or a situation which seems to defy logic or intuition...
in game theory
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
, has been described as: A losing strategy that wins. It is named after its creator, Spanish
Spain
Spain , officially the Kingdom of Spain languages]] under the European Charter for Regional or Minority Languages. In each of these, Spain's official name is as follows:;;;;;;), is a country and member state of the European Union located in southwestern Europe on the Iberian Peninsula...
physicist
Physicist
A physicist is a scientist who studies or practices physics. Physicists study a wide range of physical phenomena in many branches of physics spanning all length scales: from sub-atomic particles of which all ordinary matter is made to the behavior of the material Universe as a whole...
Juan Parrondo
J. M. R. Parrondo
Juan Manuel Rodríguez Parrondo is a Spanish physicist best known for the strikingly counterintuitive Parrondo's paradox, where switching between losing strategies can, in some cases, win on average. In 1996, he developed games of chance, now called Parrondo's games, that exhibited this apparently...
, who discovered the paradox in 1996. A more explanatory description is:
- Given two games, each with a higher probability of losing than winning, it is possible to construct a winning strategy by playing the games alternately.
Parrondo devised the paradox in connection with his analysis of the Brownian ratchet
Brownian ratchet
In the philosophy of thermal and statistical physics, the Brownian ratchet, or Feynman-Smoluchowski ratchet is a thought experiment about an apparent perpetual motion machine first analysed in 1912 by Polish physicist Marian Smoluchowski and popularised by American Nobel laureate physicist Richard...
, a thought experiment
Thought experiment
A thought experiment or Gedankenexperiment considers some hypothesis, theory, or principle for the purpose of thinking through its consequences...
about a machine that can purportedly extract energy from random heat motions popularized by physicist Richard Feynman
Richard Feynman
Richard Phillips Feynman was an American physicist known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics and the physics of the superfluidity of supercooled liquid helium, as well as in particle physics...
.
The saw-tooth example
Now consider the game in which we alternate the two profiles while judiciously choosing the time between altering from one profile to the other in the following way.
It easily follows that eventually we will have marbles at point A, but none at point B. Hence for a problem defined with having marbles at point A being a win and having marbles at point B a loss, we clearly win by playing two losing games.
The coin-tossing example
A second example of Parrondo's paradox is drawn from the field of gambling. Consider playing two games, Game A and Game B with following rules. For convenience, define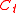 to be our capital at time t, immediately before we play a game.
- Winning a game earns us $1 and losing requires us to surrender $1. It follows that
if we win at step t and 
if we lose at step t. - In Game A, we toss a biased coin, Coin 1, with probability of winning
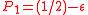. If 
, this is clearly a losing game in the long run. - In Game B, we first determine if our capital is a multiple of some integer
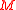. If it is, we toss a biased coin, Coin 2, with probability of winning 
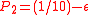. If it is not, we toss another biased coin, Coin 3, with probability of winning 
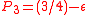. The role of modulo 
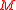provides the periodicity as in the ratchet teeth.
It is clear that by playing Game A, we will almost surely lose in the long run. Harmer and Abbott show via simulation that if
and Game B is an almost surely losing game as well. In fact, Game B is a Markov chainMarkov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
, and an analysis of its state transition matrix (again with M=3) shows that the steady state probability of using coin 2 is 0.3836, and that of using coin 3 is 0.6164. As coin 2 is selected nearly 40% of the time, it has a disproportionate influence on the payoff from Game B, and results in it being a losing game.
However, when these two losing games are played in some alternating sequence - e.g. two games of A followed by two games of B (AABBAABB....), the combination of the two games is, paradoxically, a winning game. Not all alternating sequences of A and B result in winning games. For example, one game of A followed by one game of B (ABABAB...) is a losing game, while one game of A followed by two games of B (ABBABB....) is a winning game. This coin-tossing example has become the canonical illustration of Parrondo's paradox – two games, both losing when played individually, become a winning game when played in a particular alternating sequence. The apparent paradox has been explained using a number of sophisticated approaches, including Markov chains, flashing ratchets, Simulated Annealing and information theory. One way to explain the apparent paradox is as follows:
- While Game B is a losing game under the probability distribution that results for
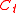modulo 
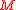when it is played individually (
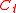modulo 
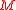is the remainder when 
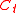is divided 
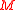), it can be a winning game under other distributions, as there is at least one state in which its expectation is positive. - As the distribution of outcomes of Game B depend on the player's capital, the two games cannot be independent. If they were, playing them in any sequence would lose as well.
The role of
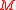now comes into sharp focus. It serves solely to induce a dependence between Games A and B, so that a player is more likely to enter states in which Game B has a positive expectation, allowing it to overcome the losses from Game A. With this understanding, the paradox resolves itself: The individual games are losing only under a distribution that differs from that which is actually encountered when playing the compound game. In summary, Parrondo's paradox is an example of how dependence can wreak havoc with probabilistic computations made under a naive assumption of independence. A more detailed exposition of this point, along with several related examples, can be found in Philips and Feldman.Application of Parrondo's paradox
Parrondo's paradox is used extensively in game theory, and its application in engineering, population dynamics, financial risk, etc, are also being looked into as demonstrated by the reading lists below.Parrondo's games are of little practical use such as for investing in stock market
Stock market
A stock market or equity market is a public entity for the trading of company stock and derivatives at an agreed price; these are securities listed on a stock exchange as well as those only traded privately.The size of the world stock market was estimated at about $36.6 trillion...
s as the original games require the payoff from at least one of the interacting games to depend on the player's capital. However, the games need not be restricted to their original form and work continues in generalizing the phenomenon. Similarities to volatility pumping and the two-envelope problem
Two envelopes problem
The two envelopes problem, also known as the exchange paradox, is a brain teaser, puzzle or paradox in logic, philosophy, probability and recreational mathematics, of special interest in decision theory and for the Bayesian interpretation of probability theory...
have been pointed out. Simple finance textbook models of security returns have been used to prove that individual investments with negative median long-term returns may be easily combined into diversified portfolios with positive median long-term returns. Similarly, a model that is often used to illustrate optimal betting rules has been used to prove that splitting bets between multiple games can turn a negative median long-term return into a positive one.
Name
In the early literature on Parrondo's paradox, it was debated whether the word 'paradox' is an appropriate description given that the Parrondo effect can be understood in mathematical terms. The 'paradoxical' effect can be mathematically explained in terms of a convex linear combination.However, Derek Abbott
Derek Abbott
Derek Abbott is a physicist and electronic engineer. He is a Professor of Electrical and Electronic Engineering at the University of Adelaide, Australia...
, a leading Parrondo's paradox researcher provides the following answer regarding the use of the word 'paradox' in this context:
See also
- Ratchet effectRatchet effectA metaphorical ratchet effect is an instance of the restrained ability of human processes to be reversed once a specific thing has happened, analogous with the mechanical ratchet that holds the spring tight as a clock is wound up...
- Brownian ratchetBrownian ratchetIn the philosophy of thermal and statistical physics, the Brownian ratchet, or Feynman-Smoluchowski ratchet is a thought experiment about an apparent perpetual motion machine first analysed in 1912 by Polish physicist Marian Smoluchowski and popularised by American Nobel laureate physicist Richard...
- Statistical mechanicsStatistical mechanicsStatistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
- List of paradoxes
- Brazil nut effectBrazil nut effectGranular convection is a phenomenon where granular material subjected to shaking or vibration will exhibit circulation patterns similar to types of fluid convection...
- Game theoryGame theoryGame theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
Further reading
- John Allen PaulosJohn Allen PaulosJohn Allen Paulos is a professor of mathematics at Temple University in Philadelphia who has gained fame as a writer and speaker on mathematics and the importance of mathematical literacy...
, A Mathematician Plays the Stock Market, Basic Books, 2004, ISBN 0-465-05481-1. - Neil F. JohnsonNeil F. JohnsonNeil Fraser Johnson is a Professor of physics notable for his work in complexity theory and complex systems, spanning quantum information, econophysics, and condensed matter physics. He is also notable for his book Financial Market Complexity published by Oxford University Press, and for his...
, Paul Jefferies, Pak Ming Hui, Financial Market Complexity, Oxford University Press, 2003, ISBN 0-19-852665-2. - Ning Zhong and Jiming Liu, Intelligent Agent Technology: Research and Development, World Scientific, 2001, ISBN 981-02-4706-0.
- Elka Korutcheva and Rodolfo Cuerno, Advances in Condensed Matter and Statistical Physics, Nova Publishers, 2004, ISBN 1-59033-899-5.
- Maria Carla Galavotti, Roberto Scazzieri, and Patrick Suppes, Reasoning, Rationality, and Probability, Center for the Study of Language and Information, 2008, ISBN 1-57586-557-2.
- Derek AbbottDerek AbbottDerek Abbott is a physicist and electronic engineer. He is a Professor of Electrical and Electronic Engineering at the University of Adelaide, Australia...
and Laszlo B. KishLaszlo B. KishLászló Bela Kish is a physicist and professor of Electrical and Computer Engineering at Texas A&M University. His activities include a wide range of issues surrounding the physics and technical applications of stochastic fluctuations in physical, biological and technological systems, including...
, Unsolved Problems of Noise and Fluctuations, American Institute of Physics, 2000, ISBN 1-56396-826-6. - Visarath In, Patrick Longhini, and Antonio Palacios, Applications of Nonlinear Dynamics: Model and Design of Complex Systems, Springer, 2009, ISBN 3-540-85631-5.
- Marc Moore, Constance van Eeden, Sorana Froda, and Christian Léger, Mathematical Statistics and Applications: Festschrift for Constance van Eeden, IMS, 2003, ISBN 0-940600-57-9.
- Ehrhard Behrends, Fünf Minuten Mathematik: 100 Beiträge der Mathematik-Kolumne der Zeitung Die Welt, Vieweg+Teubner Verlag, 2006, ISBN 3-8348-0082-1.
- Lutz Schimansky-Geier, Noise in Complex Systems and Stochastic Dynamics, SPIE, 2003, ISBN 0-8194-4974-1.
- Susan Shannon, Artificial Intelligence and Computer Science, Nova Science Publishers, 2005, ISBN 1-59454-411-5.
- Eric W. WeissteinEric W. WeissteinEric W. Weisstein is an encyclopedist who created and maintains MathWorld and Eric Weisstein's World of Science . He currently works for Wolfram Research, Inc.-Education:...
, CRC Concise Encyclopedia of Mathematics, CRC Press, 2003, ISBN 1-58488-347-2. - David Reguera, José M. G. Vilar, and José-Miguel Rubí, Statistical Mechanics of Biocomplexity, Springer, 1999, ISBN 3-540-66245-6.
- Sergey M. BezrukovSergey M. BezrukovSergey M. Bezrukov is a biophysicist notable for his work on ion channels and stochastic resonance.-Education:He received his MS in Electronics and Theoretical Physics fromSaint Petersburg Polytechnical University, 1973; and he obtained his PhD under...
, Unsolved Problems of Noise and Fluctuations, Springer, 2003, ISBN 0-7354-0127-6. - Julián Chela Flores, Tobias C. Owen, and F. Raulin, First Steps in the Origin of Life in the Universe, Springer, 2001, ISBN 1-4020-0077-4.
- Tönu Puu and Irina Sushko, Business Cycle Dynamics: Models and Tools, Springer, 2006, ISBN 3-540-32167-5.
- Andrzej S. Nowak and Krzysztof Szajowski, Advances in Dynamic Games: Applications to Economics, Finance, Optimization, and Stochastic Control, Birkhäuser, 2005, ISBN 0-8176-4362-1.
- Cristel Chandre, Xavier Leoncini, and George M. Zaslavsky, Chaos, Complexity and Transport: Theory and Applications, World Scientific, 2008, ISBN 981-281-879-0.
- Richard A. EpsteinRichard A. EpsteinRichard Arnold Epstein , also known under the pseudonym E. P. Stein, is a notable American game theorist.-Education:...
, The Theory of Gambling and Statistical Logic (Second edition), Academic Press, 2009, ISBN 0-12-374940-9. - Clifford A. PickoverClifford A. PickoverClifford A. Pickover is an American author, editor, and columnist in the fields of science, mathematics, and science fiction, and is employed at the IBM Thomas J. Watson Research Center in Yorktown, New York.- Biography :He received his Ph.D...
, The Math Book, Sterling, 2009, ISBN 1-4027-5796-4.
External links
- Parrondo J. M. R. Parrondo's paradoxical games
- Nature news article on Parrondo's paradox
- Alternate game play ratchets up winnings: It's the law
- Official Parrondo's paradox page
- Parrondo's Paradox - A Simulation
- The Wizard of Odds on Parrondo's Paradox
- Parrondo's Paradox at Wolfram
- Online Parrondo simulator
- Parrondo's paradox at Maplesoft
- Donald Catlin on Parrondo's paradox
- Parrondo's paradox and poker
- Parrondo's paradox and epistemology
- A Parrondo's paradox resource
- Optimal adaptive strategies and Parrondo
- Behrends on Parrondo
- God doesn't shoot craps
- Parrondo's paradox in chemistry
- Parrondo's paradox in genetics
- Parrondo effect in quantum mechanics
- Financial diversification and Parrondo