
Parity-check matrix
Encyclopedia
In coding theory
, a parity-check matrix of a linear block code C
is a generator matrix
of the dual code. As such, a codeword c is in C if and only if
the matrix-vector product Hc=0.
The rows of a parity check matrix are parity checks on the codewords of a code. That is, they show how linear combinations of certain digits of each codeword equal zero. For example, the parity check matrix
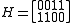
specifies that for each codeword, digits 1 and 2 should sum to zero (according to the second row) and digits 3 and 4 should sum to zero (according to the first row).
(and vice-versa). If the generator matrix for an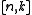 -code is in standard form
-code is in standard form
then the parity check matrix is given by
because
Negation is performed in the finite field mod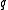 . Note that if the characteristic
. Note that if the characteristic
of the underlying field is 2 (i.e.,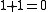 in that field), as in binary code
in that field), as in binary code
s, then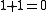 , so the negation is unnecessary.
, so the negation is unnecessary.
For example, if a binary code has the generator matrix
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
, a parity-check matrix of a linear block code C
is a generator matrix
Generator matrix
In coding theory, a generator matrix is a basis for a linear code, generating all its possible codewords.If the matrix is G and the linear code is C,where w is a codeword of the linear code C, c is a row vector, and a bijection exists between w and c. A generator matrix for an q-code has...
of the dual code. As such, a codeword c is in C if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the matrix-vector product Hc=0.
The rows of a parity check matrix are parity checks on the codewords of a code. That is, they show how linear combinations of certain digits of each codeword equal zero. For example, the parity check matrix
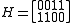
specifies that for each codeword, digits 1 and 2 should sum to zero (according to the second row) and digits 3 and 4 should sum to zero (according to the first row).
Creating a parity check matrix
The parity check matrix for a given code can be derived from its generator matrixGenerator matrix
In coding theory, a generator matrix is a basis for a linear code, generating all its possible codewords.If the matrix is G and the linear code is C,where w is a codeword of the linear code C, c is a row vector, and a bijection exists between w and c. A generator matrix for an q-code has...
(and vice-versa). If the generator matrix for an
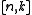 -code is in standard form
-code is in standard form
-
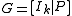 ,
,
then the parity check matrix is given by
-
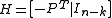 ,
,
because
-
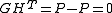 .
.
Negation is performed in the finite field mod
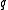 . Note that if the characteristic
. Note that if the characteristicCharacteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
of the underlying field is 2 (i.e.,
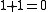 in that field), as in binary code
in that field), as in binary codeBinary code
A binary code is a way of representing text or computer processor instructions by the use of the binary number system's two-binary digits 0 and 1. This is accomplished by assigning a bit string to each particular symbol or instruction...
s, then
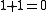 , so the negation is unnecessary.
, so the negation is unnecessary.For example, if a binary code has the generator matrix
-
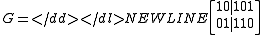
The parity check matrix becomes
-

For any valid codeword ,
, 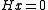 . For any invalid codeword
. For any invalid codeword 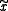 , the syndrome
, the syndrome 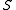 satisfies
satisfies 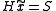 .
.
-

