
Oscillation (differential equation)
Encyclopedia
In mathematics
, in the field of ordinary differential equation
s, a non trivial solution to an ordinary differential equation
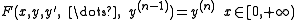
is called oscillating if it has an infinite number of roots, otherwise it is called non-oscillating. The differential equation is called oscillating if it has an oscillating solution.
The number of roots carries also information on the spectrum
of associated boundary value problem
s.

is oscillating as sin(x) is a solution.
the question about oscillation/non-oscillation answers the question whether the eigenvalues accumulate at the bottom of the continuous spectrum.
–Simon
–Teschl
showed that the number of roots of the Wronski determinant of two eigenfunctions of a Sturm–Liouville problem gives the number of eigenvalues between the corresponding eigenvalues. It was later on generalized by Krüger–Teschl to the case of two eigenfunctions of two different Sturm–Liouville problems. The investigation of the number of roots of the Wronski determinant of two solutions is known as relative oscillation theory.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the field of ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s, a non trivial solution to an ordinary differential equation
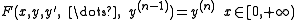
is called oscillating if it has an infinite number of roots, otherwise it is called non-oscillating. The differential equation is called oscillating if it has an oscillating solution.
The number of roots carries also information on the spectrum
Spectrum (functional analysis)
In functional analysis, the concept of the spectrum of a bounded operator is a generalisation of the concept of eigenvalues for matrices. Specifically, a complex number λ is said to be in the spectrum of a bounded linear operator T if λI − T is not invertible, where I is the...
of associated boundary value problem
Boundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
s.
Examples
The differential equation
is oscillating as sin(x) is a solution.
Connection with spectral theory
Oscillation theory was initiated by Jacques Charles François Sturm in his investigations of Sturm–Liouville problems from 1836. There he showed that the n'th eigenfunction of a Sturm–Liouville problem has precisely n-1 roots. For the one-dimensional Schrödinger equationSchrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
the question about oscillation/non-oscillation answers the question whether the eigenvalues accumulate at the bottom of the continuous spectrum.
Relative oscillation theory
In 1996 GesztesyFritz Gesztesy
Friedrich „Fritz“ Gesztesy is a well-known Austrian-American mathematical physicist and Professor of Mathematics at the University of Missouri, known for his important contributions in spectral theory, functional analysis, nonrelativistic quantum mechanics , and completely integrable systems...
–Simon
Barry Simon
Barry Simon is an eminent American mathematical physicist and the IBM Professor of Mathematics and Theoretical Physics at Caltech, known for his prolific contributions in spectral theory, functional analysis, and nonrelativistic quantum mechanics , including the connections to atomic and...
–Teschl
Gerald Teschl
Gerald Teschl is an Austrian mathematical physicist and Professor of Mathematics.He is working in the area of mathematical physics; in particular direct and inverse spectral theory with application to completely integrable partial differential equations .-Career:After studying physics at the Graz...
showed that the number of roots of the Wronski determinant of two eigenfunctions of a Sturm–Liouville problem gives the number of eigenvalues between the corresponding eigenvalues. It was later on generalized by Krüger–Teschl to the case of two eigenfunctions of two different Sturm–Liouville problems. The investigation of the number of roots of the Wronski determinant of two solutions is known as relative oscillation theory.
See also
Classical results in oscillation theory are:- Kneser theoremKneser theoremIn mathematics, in the field of ordinary differential equations, the Kneser theorem, named after Adolf Kneser, provides criteria to decide whether a differential equation is oscillating or not.- Statement of the theorem :...
- Sturm–Picone comparison theorem
- Sturm separation theoremSturm separation theoremIn mathematics, in the field of ordinary differential equations, Sturm separation theorem, named after Jacques Charles François Sturm, describes the location of roots of homogeneous second order linear differential equations...

