Oriented projective geometry
Encyclopedia
Oriented projective geometry is an oriented
version of real projective geometry
.
Whereas the real projective plane
describes the set of all unoriented lines through the origin in R3, the oriented projective plane describes lines with a given orientation. There are applications in computer graphics
and computer vision
where it is necessary to distinguish between rays light being emitted or absorbed by a point.
Elements in an oriented projective space are defined using signed homogeneous coordinates
. Let
be the set of elements of 
excluding the origin.
These spaces can be viewed as extensions of euclidean space
.
can be viewed as the union of two copies of 
, the sets (x,1) and (x,-1), plus two additional points at infinity, (1,0) and (-1,0). Likewise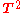 
can be view two copies of 
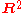, (x,y,1) and (x,y,-1), plus one copy of 
(x,y,0).
An alternative way to view the spaces is as points on the circle or sphere, given by the points (x,y,w) with
Distances between two points
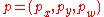
and
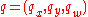
in
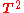
can be defined as elements in
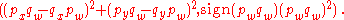
Orientability
In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
version of real projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
.
Whereas the real projective plane
Real projective plane
In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
describes the set of all unoriented lines through the origin in R3, the oriented projective plane describes lines with a given orientation. There are applications in computer graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
and computer vision
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
where it is necessary to distinguish between rays light being emitted or absorbed by a point.
Elements in an oriented projective space are defined using signed homogeneous coordinates
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
. Let
be the set of elements of excluding the origin.
- Oriented projective line,
: 
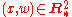, with the equivalence relationEquivalence relationIn mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
for all 
. - Oriented projective plane,
: 
, with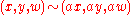 
for all 
.
These spaces can be viewed as extensions of euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
.
can be viewed as the union of two copies of , the sets (x,1) and (x,-1), plus two additional points at infinity, (1,0) and (-1,0). Likewise 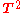can be view two copies of 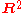, (x,y,1) and (x,y,-1), plus one copy of (x,y,0).An alternative way to view the spaces is as points on the circle or sphere, given by the points (x,y,w) with
- x2+y2+z2=1.
Distances between two points
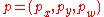
and
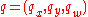
in
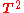
can be defined as elements in