
Orbit (control theory)
Encyclopedia
The notion of orbit
of a control system used in mathematical control theory
is a particular case of the notion of orbit in group theory.
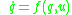
be a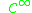 control system, where
control system, where
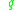
belongs to a finite-dimensional manifold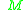 and
and 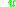 belongs to a control set
belongs to a control set 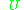 . Consider the family
. Consider the family 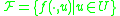
and assume that every vector field in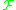 is complete.
is complete.
For every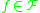 and every real
and every real 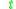 , denote by
, denote by 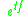 the flow
the flow
of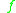 at time
at time 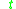 .
.
The orbit of the control system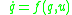 through a point
through a point 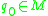 is the subset
is the subset 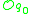 of
of 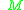 defined by
defined by

Remarks
The difference between orbits and attainable sets is that, whereas for attainable sets only forward-in-time motions are allowed, both forward and backward motions are permitted for orbits.
In particular, if the family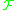 is symmetric (i.e.,
is symmetric (i.e., 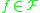 if and only if
if and only if 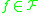 ), then orbits and attainable sets coincide.
), then orbits and attainable sets coincide.
The hypothesis that every vector field of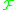 is complete simplifies the notations but can be dropped. In this case one has to replace flows of vector fields by local versions of them.
is complete simplifies the notations but can be dropped. In this case one has to replace flows of vector fields by local versions of them.
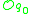 is an immersed submanifold of
is an immersed submanifold of 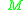 .
.
The tangent space to the orbit
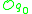 at a point
at a point 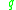 is the linear subspace of
is the linear subspace of 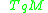 spanned by
spanned by
the vectors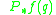 where
where  denotes the pushforward of
denotes the pushforward of 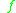 by
by 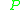 ,
, 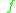 belongs to
belongs to 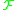 and
and 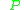 is a diffeomorphism of
is a diffeomorphism of 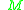 of the form
of the form  with
with  and
and 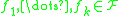 .
.
If all the vector fields of the family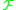 are analytic, then
are analytic, then  where
where 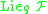 is the evaluation at
is the evaluation at 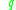 of the Lie algebra
of the Lie algebra
generated by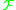 with respect to the Lie bracket of vector fields
with respect to the Lie bracket of vector fields
.
Otherwise, the inclusion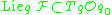 holds true.
holds true.
 for every
for every 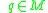 and if
and if 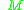 is connected, then each orbit is equal to the whole manifold
is connected, then each orbit is equal to the whole manifold 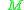 .
.
Orbit
In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
of a control system used in mathematical control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
is a particular case of the notion of orbit in group theory.
Definition
Let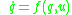
be a
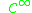 control system, where
control system, where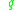
belongs to a finite-dimensional manifold
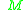 and
and 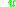 belongs to a control set
belongs to a control set 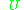 . Consider the family
. Consider the family 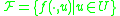
and assume that every vector field in
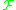 is complete.
is complete.For every
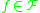 and every real
and every real 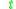 , denote by
, denote by 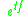 the flow
the flowVector flow
In mathematics, the vector flow refers to a set of closely related concepts of the flow determined by a vector field. These appear in a number of different contexts, including differential topology, Riemannian geometry and Lie group theory...
of
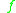 at time
at time 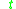 .
.The orbit of the control system
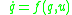 through a point
through a point 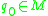 is the subset
is the subset 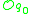 of
of 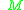 defined by
defined by
Remarks
The difference between orbits and attainable sets is that, whereas for attainable sets only forward-in-time motions are allowed, both forward and backward motions are permitted for orbits.
In particular, if the family
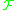 is symmetric (i.e.,
is symmetric (i.e., 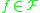 if and only if
if and only if 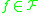 ), then orbits and attainable sets coincide.
), then orbits and attainable sets coincide.The hypothesis that every vector field of
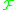 is complete simplifies the notations but can be dropped. In this case one has to replace flows of vector fields by local versions of them.
is complete simplifies the notations but can be dropped. In this case one has to replace flows of vector fields by local versions of them.Orbit theorem (Nagano-Sussmann)
Each orbit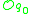 is an immersed submanifold of
is an immersed submanifold of 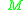 .
.The tangent space to the orbit
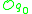 at a point
at a point 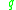 is the linear subspace of
is the linear subspace of 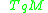 spanned by
spanned bythe vectors
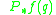 where
where  denotes the pushforward of
denotes the pushforward of 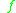 by
by 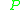 ,
, 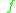 belongs to
belongs to 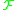 and
and 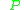 is a diffeomorphism of
is a diffeomorphism of 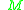 of the form
of the form  with
with  and
and 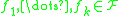 .
.If all the vector fields of the family
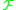 are analytic, then
are analytic, then  where
where 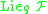 is the evaluation at
is the evaluation at 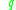 of the Lie algebra
of the Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
generated by
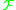 with respect to the Lie bracket of vector fields
with respect to the Lie bracket of vector fieldsLie bracket of vector fields
In the mathematical field of differential topology, the Lie bracket of vector fields, Jacobi–Lie bracket, or commutator of vector fields is a bilinear differential operator which assigns, to any two vector fields X and Y on a smooth manifold M, a third vector field denoted [X, Y]...
.
Otherwise, the inclusion
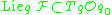 holds true.
holds true.Corollary (Rashevsky-Chow theorem)
If for every
for every 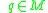 and if
and if 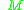 is connected, then each orbit is equal to the whole manifold
is connected, then each orbit is equal to the whole manifold 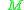 .
.

