
Normal polytope
Encyclopedia
In mathematics
, specifically in combinatorial commutative algebra
, a convex lattice polytope
P is called normal if it has the following property: given any positive integer n, every lattice point of the dilation nP, obtained from P by scaling its vertices by the factor n and taking the convex hull
of the resulting points, can be written as the sum of exactly n lattice points in P. This property plays an important role in the theory of toric varieties, where it corresponds to projective normality of the toric variety determined by P.
in Rk with the vertices at the origin and along the unit coordinate vectors is normal.
M can be embedded into an abelian group
. More precisely, the canonical map from M into its Grothendieck group
K(M) is an embedding. Define the normalization of M to be the set
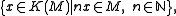
where nx here means x added to itself n times. If M is equal to its normalization, then we say that M is a normal monoid. For example, the monoid Nn consisting of n-tuples of natural numbers is a normal monoid, with the Grothendieck group Zn.
For a polytope P ⊆ Rk, lift P into Rk+1 so that it lies in the hyperplane xk+1 = 1, and let C(P) be the set of all linear combinations with nonnegative coefficients of points in (P,1). Then C(P) is a convex cone
,
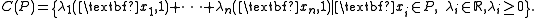
If P is a convex lattice polytope, then it follows from Gordan's lemma that the intersection of C(P) with the lattice Zk+1 is a finitely generated (commutative, cancellative) monoid. One can prove that P is a normal polytope if and only if this monoid is normal.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in combinatorial commutative algebra
Combinatorial commutative algebra
Combinatorial commutative algebra is a relatively new, rapidly developing mathematical discipline. As the name implies, it lies at the intersection of two more established fields, commutative algebra and combinatorics, and frequently uses methods of one to address problems arising in the other...
, a convex lattice polytope
Convex lattice polytope
A convex lattice polytope is a geometric object playing an important role in discrete geometry and combinatorial commutative algebra. It is a polytope in a Euclidean space Rn which is a convex hull of finitely many points in the integer lattice Zn ⊂ Rn...
P is called normal if it has the following property: given any positive integer n, every lattice point of the dilation nP, obtained from P by scaling its vertices by the factor n and taking the convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of the resulting points, can be written as the sum of exactly n lattice points in P. This property plays an important role in the theory of toric varieties, where it corresponds to projective normality of the toric variety determined by P.
Example
The simplexSimplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
in Rk with the vertices at the origin and along the unit coordinate vectors is normal.
Relation to normal monoids
Any cancellative commutative monoidMonoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
M can be embedded into an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
. More precisely, the canonical map from M into its Grothendieck group
Grothendieck group
In mathematics, the Grothendieck group construction in abstract algebra constructs an abelian group from a commutative monoid in the best possible way...
K(M) is an embedding. Define the normalization of M to be the set
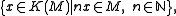
where nx here means x added to itself n times. If M is equal to its normalization, then we say that M is a normal monoid. For example, the monoid Nn consisting of n-tuples of natural numbers is a normal monoid, with the Grothendieck group Zn.
For a polytope P ⊆ Rk, lift P into Rk+1 so that it lies in the hyperplane xk+1 = 1, and let C(P) be the set of all linear combinations with nonnegative coefficients of points in (P,1). Then C(P) is a convex cone
Convex cone
In linear algebra, a convex cone is a subset of a vector space over an ordered field that is closed under linear combinations with positive coefficients.-Definition:...
,
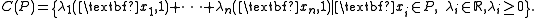
If P is a convex lattice polytope, then it follows from Gordan's lemma that the intersection of C(P) with the lattice Zk+1 is a finitely generated (commutative, cancellative) monoid. One can prove that P is a normal polytope if and only if this monoid is normal.

