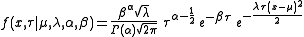Normal-gamma distribution
Encyclopedia
In probability theory
and statistics
, the normal-gamma distribution is a bivariate four-parameter family of continuous probability distribution
s. It is the conjugate prior
of a normal distribution with unknown mean
and precision
.

has a normal distribution with mean
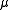 and variance
and variance
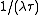 , where
, where
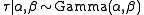
has a gamma distribution. Then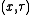
has a normal-gamma distribution, denoted as
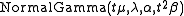
over is a gamma distribution, and the conditional distribution
is a gamma distribution, and the conditional distribution
over given
given  is a Gaussian distribution. The marginal distribution
is a Gaussian distribution. The marginal distribution
over is a three-parameter Student's t-distribution.
is a three-parameter Student's t-distribution.
Presume the following hierarchy for a normal random variable X with unknown mean and precision
and precision 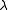 .
.
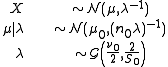
Where:
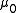 is the prior mean
is the prior mean
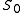 is the prior sum of squared errors
is the prior sum of squared errors
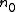 is the prior sample size
is the prior sample size
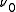 is the prior degrees of freedom
is the prior degrees of freedom
Note the joint distribution of the parameters is Normal-Gamma. The posterior distribution of the parameters can be analytically determined by Bayes' rule working with the likelihood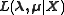 , and the prior
, and the prior 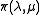 .
.
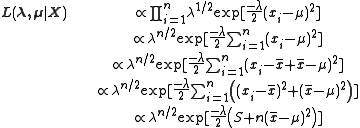
where , the sum of squared errors.
, the sum of squared errors.
Now consider the prior,
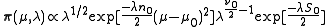
The posterior distribution of the parameters is proportional to the prior times the likelihood.
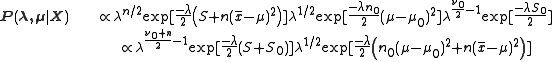
Notice the right half begins to look like the kernel of a normal pdf and the left like a gamma. After a bit of juggling and completing the square the result will appear.
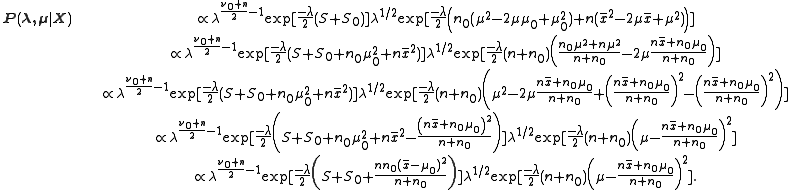
This is a normal gamma pdf with parameters
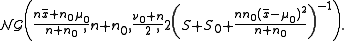
The reference prior is the limiting case as
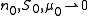
and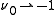
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the normal-gamma distribution is a bivariate four-parameter family of continuous probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s. It is the conjugate prior
Conjugate prior
In Bayesian probability theory, if the posterior distributions p are in the same family as the prior probability distribution p, the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood...
of a normal distribution with unknown mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
and precision
Precision (statistics)
In statistics, the term precision can mean a quantity defined in a specific way. This is in addition to its more general meaning in the contexts of accuracy and precision and of precision and recall....
.
Definition
Suppose
has a normal distribution with mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
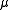 and variance
and varianceVariance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
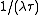 , where
, where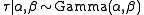
has a gamma distribution. Then
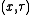
has a normal-gamma distribution, denoted as

Probability density function
Scaling
For any t > 0, tX is distributed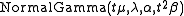
Marginal distributions
By construction, the marginal distributionMarginal distribution
In probability theory and statistics, the marginal distribution of a subset of a collection of random variables is the probability distribution of the variables contained in the subset. The term marginal variable is used to refer to those variables in the subset of variables being retained...
over
 is a gamma distribution, and the conditional distribution
is a gamma distribution, and the conditional distributionConditional distribution
Given two jointly distributed random variables X and Y, the conditional probability distribution of Y given X is the probability distribution of Y when X is known to be a particular value...
over
 given
given  is a Gaussian distribution. The marginal distribution
is a Gaussian distribution. The marginal distributionMarginal distribution
In probability theory and statistics, the marginal distribution of a subset of a collection of random variables is the probability distribution of the variables contained in the subset. The term marginal variable is used to refer to those variables in the subset of variables being retained...
over
 is a three-parameter Student's t-distribution.
is a three-parameter Student's t-distribution.Posterior distribution of the parameters
Form of the posterior for a Normal random variable with a Normal-Gamma prior:Presume the following hierarchy for a normal random variable X with unknown mean
 and precision
and precision 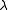 .
.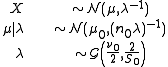
Where:
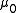 is the prior mean
is the prior mean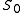 is the prior sum of squared errors
is the prior sum of squared errors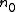 is the prior sample size
is the prior sample size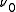 is the prior degrees of freedom
is the prior degrees of freedomNote the joint distribution of the parameters is Normal-Gamma. The posterior distribution of the parameters can be analytically determined by Bayes' rule working with the likelihood
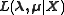 , and the prior
, and the prior 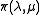 .
.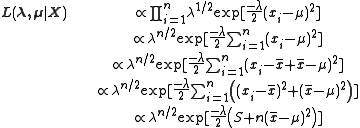
where
 , the sum of squared errors.
, the sum of squared errors.Now consider the prior,
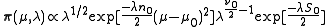
The posterior distribution of the parameters is proportional to the prior times the likelihood.
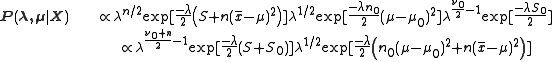
Notice the right half begins to look like the kernel of a normal pdf and the left like a gamma. After a bit of juggling and completing the square the result will appear.
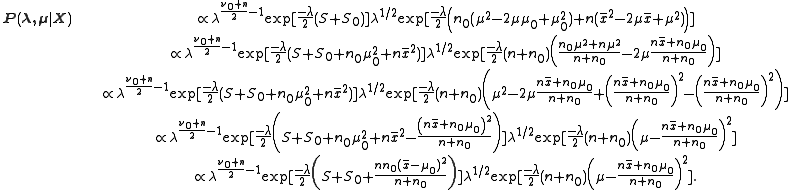
This is a normal gamma pdf with parameters
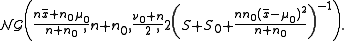
The reference prior is the limiting case as
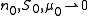
and
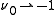
Generating normal-gamma random variates
Generation of random variates is straightforward:- Sample
 from a gamma distribution with parameters
from a gamma distribution with parameters  and
and 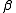
- Sample
 from a normal distribution with mean
from a normal distribution with mean 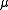 and variance
and variance 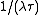
Related distributions
- The normal-scaled inverse gamma distribution is essentially the same distribution parameterized by variance rather than precision
- The Normal-exponential-gamma distributionNormal-exponential-gamma distributionIn probability theory and statistics, the normal-exponential-gamma distribution is a three-parameter family of continuous probability distributions...