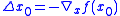Nonlinear conjugate gradient method
Encyclopedia
In numerical optimization, the nonlinear conjugate gradient method generalizes the conjugate gradient method
to nonlinear optimization. For a quadratic function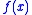 :
:
The minimum of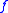 is obtained when the gradient
is obtained when the gradient
is 0:
Whereas linear conjugate gradient seeks a solution to the linear equation
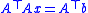 , the nonlinear conjugate gradient method is generally
, the nonlinear conjugate gradient method is generally
used to find the local minimum of a nonlinear function
using its gradient
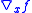 alone. It works when the function is approximately quadratic near the minimum, which is the case when the function is twice differentiable at the minimum.
alone. It works when the function is approximately quadratic near the minimum, which is the case when the function is twice differentiable at the minimum.
Given a function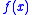 of
of  variables to minimize, its gradient
variables to minimize, its gradient 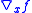 indicates the direction of maximum increase.
indicates the direction of maximum increase.
One simply starts in the opposite (steepest descent) direction:
with an adjustable step length and performs a line search in this direction until it reaches the minimum of
and performs a line search in this direction until it reaches the minimum of 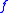 :
:
After this first iteration in the steepest direction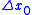 , the following steps constitute one iteration of moving along a subsequent conjugate direction
, the following steps constitute one iteration of moving along a subsequent conjugate direction 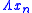 , where
, where  :
:
With a pure quadratic function the minimum is reached within N iterations (excepting roundoff error), but a non-quadratic function will make slower progress. Subsequent search directions lose conjugacy requiring the search direction to be reset to the steepest descent direction at least every N iterations, or sooner if progress stops. However resetting every iteration turns the method into steepest descent. The algorithm stops when it finds the minimum, determined when no progress is made after a direction reset (i.e. in the steepest descent direction), or when some tolerance criterion is reached.
Within a linear approximation, the parameters and
and 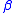 are the same as in the
are the same as in the
linear conjugate gradient method but have been obtained with line searches.
The conjugate gradient method can follow narrow (ill-conditioned) valleys where the steepest descent method slows down and follows a criss-cross pattern.
Three of the best known formulas for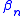 are titled Fletcher-Reeves (FR), Polak-Ribière (PR), and Hestenes-Stiefel (HS) after their developers. They are given by the following formulas:
are titled Fletcher-Reeves (FR), Polak-Ribière (PR), and Hestenes-Stiefel (HS) after their developers. They are given by the following formulas:
Conjugate gradient method
In mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is symmetric and positive-definite. The conjugate gradient method is an iterative method, so it can be applied to sparse systems that are too...
to nonlinear optimization. For a quadratic function
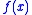 :
:
The minimum of
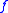 is obtained when the gradient
is obtained when the gradientGradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
is 0:
-
-
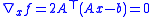 .
.
-
Whereas linear conjugate gradient seeks a solution to the linear equation
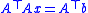 , the nonlinear conjugate gradient method is generally
, the nonlinear conjugate gradient method is generallyused to find the local minimum of a nonlinear function
using its gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
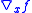 alone. It works when the function is approximately quadratic near the minimum, which is the case when the function is twice differentiable at the minimum.
alone. It works when the function is approximately quadratic near the minimum, which is the case when the function is twice differentiable at the minimum.Given a function
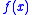 of
of  variables to minimize, its gradient
variables to minimize, its gradient 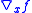 indicates the direction of maximum increase.
indicates the direction of maximum increase.One simply starts in the opposite (steepest descent) direction:
with an adjustable step length
 and performs a line search in this direction until it reaches the minimum of
and performs a line search in this direction until it reaches the minimum of 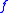 :
:
-
-
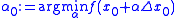 ,
, -

-
After this first iteration in the steepest direction
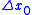 , the following steps constitute one iteration of moving along a subsequent conjugate direction
, the following steps constitute one iteration of moving along a subsequent conjugate direction 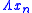 , where
, where  :
:
- Calculate the steepest direction:
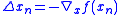 ,
, - Compute
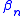 according to one of the formulas below,
according to one of the formulas below, - Update the conjugate direction:
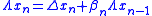
- Perform a line search: optimize
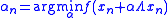 ,
, - Update the position:
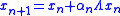 ,
,
With a pure quadratic function the minimum is reached within N iterations (excepting roundoff error), but a non-quadratic function will make slower progress. Subsequent search directions lose conjugacy requiring the search direction to be reset to the steepest descent direction at least every N iterations, or sooner if progress stops. However resetting every iteration turns the method into steepest descent. The algorithm stops when it finds the minimum, determined when no progress is made after a direction reset (i.e. in the steepest descent direction), or when some tolerance criterion is reached.
Within a linear approximation, the parameters
 and
and 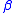 are the same as in the
are the same as in thelinear conjugate gradient method but have been obtained with line searches.
The conjugate gradient method can follow narrow (ill-conditioned) valleys where the steepest descent method slows down and follows a criss-cross pattern.
Three of the best known formulas for
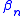 are titled Fletcher-Reeves (FR), Polak-Ribière (PR), and Hestenes-Stiefel (HS) after their developers. They are given by the following formulas:
are titled Fletcher-Reeves (FR), Polak-Ribière (PR), and Hestenes-Stiefel (HS) after their developers. They are given by the following formulas:
- Fletcher–Reeves:
-
-
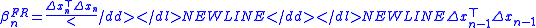
- Polak–Ribière:
-
-
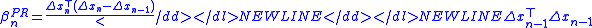
- Hestenes-Stiefel:
-
-
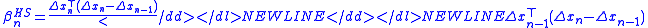 .
.
These formulas are equivalent for a quadratic function, but for nonlinear optimization the preferred formula is a matter of heuristics or taste. A popular choice is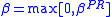 which provides a direction reset automatically.
which provides a direction reset automatically.
Newton based methods - Newton-Raphson Algorithm, Quasi-Newton methods (e.g., BFGS methodBFGS methodIn numerical optimization, the Broyden–Fletcher–Goldfarb–Shanno method is a method for solving nonlinear optimization problems ....
) - tend to converge in fewer iterations, although each iteration typically requires more computation than a conjugate gradient iteration as Newton-like methods require computing the HessianHessianThe Hessians were 18-century German regiments hired through their rulers by the British Empire. Despite their name, they were not all from Hesse. They were not mercenaries, although their German rulers profited from their use. Though used in several conflicts including in Ireland, they are most...
(matrix of second derivatives) in addition to the gradient. Quasi-Newton methods also require more memory to operate (see also the limited memory L-BFGSL-BFGSThe limited-memory BFGS algorithm is a member of the broad family of quasi-Newton optimization methods that uses a limited memory variation of the Broyden–Fletcher–Goldfarb–Shanno update to approximate the inverse Hessian matrix...
method).
External links
- An Introduction to the Conjugate Gradient Method Without the Agonizing Pain by Jonathan Richard Shewchuk.
- Numerical Recipes in C - The Art of Scientific Computing, chapter 10, section 6: Conjugate Gradient Methods in Multidimensions; William H. Press (Editor), Saul A. Teukolsky (Editor), William T. Vetterling (Author), Brian P. Flannery (Author), Cambridge University Press; 2nd edition (1992).
-
-
-