Noether normalization lemma
Encyclopedia
In mathematics
, the Noether normalization lemma is a result of commutative algebra
, introduced in . A simple version states that for any field k, and any finitely generated
commutative k-algebra A, there exists a nonnegative integer d and algebraically independent elements y1, y2, ..., yd in A
such that A is a finitely generated module over, and hence also an integral extension of, the polynomial ring B:=k[y1, y2, ..., yd].
The integer d is uniquely determined by A: it is the Krull dimension
of A. When A is an integral domain, d is then the transcendence degree
of the field of fractions
of A over k.
The lemma can be understood geometrically. Suppose A is integral. Let B be the coordinate ring of d-dimensional affine space
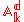, and A as the coordinate ring of some other d-dimensional affine variety X. Then the inclusion map
B → A induces a surjective finite morphism of affine varieties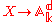
. The conclusion is that any affine variety is a branched covering
of affine space.
When k is infinite, such a branched covering map can be constructed by taking a general projection from an affine space containing X to a d-dimensional subspace.
The form of the Noether normalization lemma stated above can be used as an important step in proving Hilbert's Nullstellensatz. This gives it further geometric importance, at least formally, as the Nullstellensatz underlies the development of much of classical algebraic geometry
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Noether normalization lemma is a result of commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
, introduced in . A simple version states that for any field k, and any finitely generated
Finitely generated
In mathematics, finitely generated may refer to:* Finitely generated group* Finitely generated monoid* Finitely generated abelian group* Finitely generated module* Finitely generated ideal* Finitely generated algebra* Finitely generated space...
commutative k-algebra A, there exists a nonnegative integer d and algebraically independent elements y1, y2, ..., yd in A
such that A is a finitely generated module over, and hence also an integral extension of, the polynomial ring B:=k[y1, y2, ..., yd].
The integer d is uniquely determined by A: it is the Krull dimension
Krull dimension
In commutative algebra, the Krull dimension of a ring R, named after Wolfgang Krull , is the supremum of the number of strict inclusions in a chain of prime ideals. The Krull dimension need not be finite even for a Noetherian ring....
of A. When A is an integral domain, d is then the transcendence degree
Transcendence degree
In abstract algebra, the transcendence degree of a field extension L /K is a certain rather coarse measure of the "size" of the extension...
of the field of fractions
Field of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
of A over k.
The lemma can be understood geometrically. Suppose A is integral. Let B be the coordinate ring of d-dimensional affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
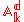, and A as the coordinate ring of some other d-dimensional affine variety X. Then the inclusion mapInclusion map
In mathematics, if A is a subset of B, then the inclusion map is the function i that sends each element, x of A to x, treated as an element of B:i: A\rightarrow B, \qquad i=x....
B → A induces a surjective finite morphism of affine varieties
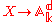. The conclusion is that any affine variety is a branched coveringBranched covering
In mathematics, branched covering is a term mainly used in algebraic geometry, to describe morphisms f from an algebraic variety V to another one W, the two dimensions being the same, and the typical fibre of f being of dimension 0....
of affine space.
When k is infinite, such a branched covering map can be constructed by taking a general projection from an affine space containing X to a d-dimensional subspace.
The form of the Noether normalization lemma stated above can be used as an important step in proving Hilbert's Nullstellensatz. This gives it further geometric importance, at least formally, as the Nullstellensatz underlies the development of much of classical algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
.