Newton-Euler equations
Encyclopedia
The Newton–Euler equations describe the combined translational and rotational dynamics of a rigid body.
With respect to a coordinate frame whose origin coincides with the body's center of mass, they can be expressed in matrix form as:
With respect to a coordinate frame whose origin coincides with the body's center of mass, they can be expressed in matrix form as:
-
where
-
= total forceForceIn physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
acting on the center of mass -
= mass of the body -
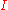= the identity matrix -
= acceleration of the center of massCenter of massIn physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body... -
= total torque (or momentMoment (physics)In physics, the term moment can refer to many different concepts:*Moment of force is the tendency of a force to twist or rotate an object; see the article torque for details. This is an important, basic concept in engineering and physics. A moment is valued mathematically as the product of the...
) acting about the center of mass -
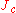= moment of inertiaMoment of inertiaIn classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
about the center of mass -
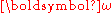= angular velocityAngular velocityIn physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
of the body
With respect to a coordinate frame that is not coincident with the center of mass, the equations assume
the more complex form:
-
where
is the location of the center of mass,
and-
denotes a skew-symmetric cross product matrix.
The inertial terms are contained in the spatial inertia matrix-
while the fictitious forces are contained in the term-
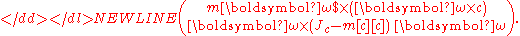
When the center of mass is not coincident with the coordinate frame
(that is, when
is nonzero), the translational and angular accelerations
(
and 
) are coupled, so that each is associated with force and torque components.
The Newton–Euler equations are used as the basis for more complicated "multi-body" formulations that describe the dynamics of systems of rigid bodies connected by joints and other constraints. Multi-body problems can be
solved by a variety of numerical algorithms.
-
-
-
-