Newey–West estimator
Encyclopedia
A Newey–West estimator is used in statistics
and econometrics
to provide an estimate of the covariance matrix
of the parameters of a regression-type
model when this model is applied in situations where the standard assumptions of regression analysis
do not apply. It was devised by Whitney K. Newey
and Kenneth D. West
in 1987, although there are a number of later variants. The estimator is used to try to overcome autocorrelation
, or correlation
, and heteroskedasticity
in the error terms
in the models. This is often used to correct the effects of correlation in the error terms in regressions applied to time series
data.
The problem in autocorrelation, often found in time series data, is that the error terms are correlated over time. This can be demonstrated in
, a matrix of sums of squares and cross products that involves 
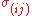and the rows of 
. The least squares estimator 
is a consistent
estimator of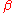
. This implies that the least squares
residual
s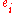
are "point-wise" consistent estimators of their population counterparts 
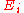. The general approach, then, will be to use 
and 
to devise an estimator of 
. What this means is that as the time between error terms increases, the correlation between the error terms decreases. The estimator thus can be used to improve the ordinary least squares
(OLS) regression
when the variables have heteroskedasticity
or autocorrelation.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
and econometrics
Econometrics
Econometrics has been defined as "the application of mathematics and statistical methods to economic data" and described as the branch of economics "that aims to give empirical content to economic relations." More precisely, it is "the quantitative analysis of actual economic phenomena based on...
to provide an estimate of the covariance matrix
Covariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
of the parameters of a regression-type
Linear regression
In statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
model when this model is applied in situations where the standard assumptions of regression analysis
Regression analysis
In statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables...
do not apply. It was devised by Whitney K. Newey
Whitney K. Newey
Whitney K. Newey is the Jane Berkowitz Carlton and Dennis William Carlton Professor of Economics at the Massachusetts Institute of Technology and a well-known econometrician. He is best known for developing, with Kenneth D...
and Kenneth D. West
Kenneth D. West
Kenneth D. West is the John D. MacArthur and Ragnar Frisch Professor of Economics in the Department of Economics at theUniversity of Wisconsin. He is best known for developing, with Whitney K...
in 1987, although there are a number of later variants. The estimator is used to try to overcome autocorrelation
Autocorrelation
Autocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
, or correlation
Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
, and heteroskedasticity
Heteroskedasticity
In statistics, a collection of random variables is heteroscedastic, or heteroskedastic, if there are sub-populations that have different variabilities than others. Here "variability" could be quantified by the variance or any other measure of statistical dispersion...
in the error terms
Errors and residuals in statistics
In statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
in the models. This is often used to correct the effects of correlation in the error terms in regressions applied to time series
Time series
In statistics, signal processing, econometrics and mathematical finance, a time series is a sequence of data points, measured typically at successive times spaced at uniform time intervals. Examples of time series are the daily closing value of the Dow Jones index or the annual flow volume of the...
data.
The problem in autocorrelation, often found in time series data, is that the error terms are correlated over time. This can be demonstrated in
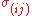, a matrix of sums of squares and cross products that involves and the rows of . The least squares estimator is a consistentConsistent estimator
In statistics, a sequence of estimators for parameter θ0 is said to be consistent if this sequence converges in probability to θ0...
estimator of
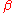. This implies that the least squaresLeast squares
The method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
residual
Errors and residuals in statistics
In statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
s
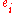are "point-wise" consistent estimators of their population counterparts 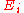. The general approach, then, will be to use and to devise an estimator of . What this means is that as the time between error terms increases, the correlation between the error terms decreases. The estimator thus can be used to improve the ordinary least squaresOrdinary least squares
In statistics, ordinary least squares or linear least squares is a method for estimating the unknown parameters in a linear regression model. This method minimizes the sum of squared vertical distances between the observed responses in the dataset and the responses predicted by the linear...
(OLS) regression
Regression analysis
In statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables...
when the variables have heteroskedasticity
Heteroskedasticity
In statistics, a collection of random variables is heteroscedastic, or heteroskedastic, if there are sub-populations that have different variabilities than others. Here "variability" could be quantified by the variance or any other measure of statistical dispersion...
or autocorrelation.
