
Neville's algorithm
Encyclopedia
In mathematics, Neville's algorithm is an algorithm used for polynomial interpolation
that was derived by the mathematician Eric Harold Neville
. Given n + 1 points, there is a unique polynomial of degree ≤ n which goes through the given points. Neville's algorithm evaluates this polynomial.
Neville's algorithm is based on the Newton form
of the interpolating polynomial and the recursion relation for the divided differences
. It is similar to Aitken's algorithm (named after Alexander Aitken
), which is nowadays not used.
This polynomial exists and it is unique. Neville's algorithm evaluates the polynomial at some point x.
Let pi,j denote the polynomial of degree j − i which goes through the points (xk, yk) for k = i, i + 1, …, j. The
pi,j satisfy the recurrence relation
This recurrence can calculate
p0,n(x),
which is the value being sought. This is Neville's algorithm.
For instance, for n = 4, one can use the recurrence to fill the triangular tableau below from the left to the right.
This process yields
p0,4(x),
the value of the polynomial going through the n + 1 data points (xi, yi) at the point x.
This algorithm needs O
(n2) floating point operations.
Polynomial interpolation
In numerical analysis, polynomial interpolation is the interpolation of a given data set by a polynomial: given some points, find a polynomial which goes exactly through these points.- Applications :...
that was derived by the mathematician Eric Harold Neville
Eric Harold Neville
Eric Harold Neville, known as E. H. Neville was an English mathematician. A heavily fictionalized portrayal of his life is rendered in the 2007 novel The Indian Clerk.-Early life and education:Eric Harold Neville was born in London on 1 January, 1889...
. Given n + 1 points, there is a unique polynomial of degree ≤ n which goes through the given points. Neville's algorithm evaluates this polynomial.
Neville's algorithm is based on the Newton form
Newton polynomial
In the mathematical field of numerical analysis, a Newton polynomial, named after its inventor Isaac Newton, is the interpolation polynomial for a given set of data points in the Newton form...
of the interpolating polynomial and the recursion relation for the divided differences
Divided differences
In mathematics divided differences is a recursive division process.The method can be used to calculate the coefficients in the interpolation polynomial in the Newton form.-Definition:Given n data points,\ldots,...
. It is similar to Aitken's algorithm (named after Alexander Aitken
Alexander Aitken
Alexander Craig Aitken was one of New Zealand's greatest mathematicians. He studied for a PhD at the University of Edinburgh, where his dissertation, "Smoothing of Data", was considered so impressive that he was awarded a DSc in 1926, and was elected a fellow of the Royal Society of Edinburgh...
), which is nowadays not used.
The algorithm
Given a set of n+1 data points (xi, yi) where no two xi are the same, the interpolating polynomial is the polynomial p of degree at most n with the property- p(xi) = yi for all i = 0,…,n
This polynomial exists and it is unique. Neville's algorithm evaluates the polynomial at some point x.
Let pi,j denote the polynomial of degree j − i which goes through the points (xk, yk) for k = i, i + 1, …, j. The
pi,j satisfy the recurrence relation
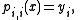 |
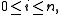 |
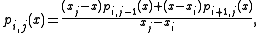 |
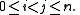 |
This recurrence can calculate
p0,n(x),
which is the value being sought. This is Neville's algorithm.
For instance, for n = 4, one can use the recurrence to fill the triangular tableau below from the left to the right.
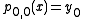 |
||||
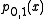 |
||||
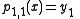 |
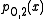 |
|||
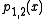 |
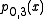 |
|||
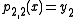 |
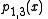 |
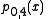 |
||
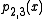 |
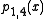 |
|||
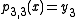 |
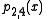 |
|||
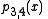 |
||||
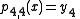 |
This process yields
p0,4(x),
the value of the polynomial going through the n + 1 data points (xi, yi) at the point x.
This algorithm needs O
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(n2) floating point operations.

