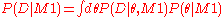Nested sampling algorithm
Encyclopedia
The nested sampling algorithm is a computational
approach to the problem of comparing models in Bayesian statistics
, developed in 2004 by physicist
John Skilling.
can be applied to a pair of competing models
and 
for data 
, one of which may be true (though which one is not known) but which both cannot simultaneously be true, as follows:
Computational
Computational may refer to:* Computer* Computational algebra* Computational Aeroacoustics* Computational and Information Systems Laboratory* Computational and Systems Neuroscience* Computational archaeology* Computational auditory scene analysis...
approach to the problem of comparing models in Bayesian statistics
Bayesian statistics
Bayesian statistics is that subset of the entire field of statistics in which the evidence about the true state of the world is expressed in terms of degrees of belief or, more specifically, Bayesian probabilities...
, developed in 2004 by physicist
Physicist
A physicist is a scientist who studies or practices physics. Physicists study a wide range of physical phenomena in many branches of physics spanning all length scales: from sub-atomic particles of which all ordinary matter is made to the behavior of the material Universe as a whole...
John Skilling.
Background
Bayes' theoremBayes' theorem
In probability theory and applications, Bayes' theorem relates the conditional probabilities P and P. It is commonly used in science and engineering. The theorem is named for Thomas Bayes ....
can be applied to a pair of competing models
and for data , one of which may be true (though which one is not known) but which both cannot simultaneously be true, as follows:-
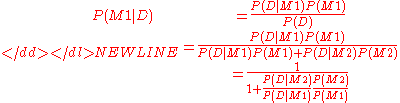
Given no a priori information in favor of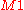
or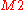 
, it is reasonable to assign prior probabilities
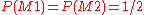, so that 
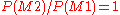. The remaining ratio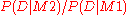 
is not so easy to evaluate since in general it requires marginalization of
nuisance parameters. Generally,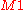
has a collection of parameters that can be
lumped together and calle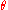d
, and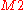 
has its own vector of parameters
that may be of different dimensionality but is still referred to as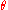
.
The marginalization for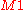
is
and likewise for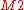
. This integral is often analytically intractable, and in these cases it is necessary to employ a numerical algorithm to find an approximation. The nested sampling algorithm was developed by John Skilling specifically to approximate these marginalization integrals, and it has the added benefit of generating samples from the posterior distribution 
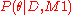. It is an alternative to methods from the Bayesian literature such as bridge sampling and defensive importance sampling.
Here is a simple version of the nested sampling algorithm, followed by a
description of how it computes the marginal probability density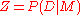
where
is 
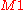or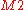 
:
Start with
points 
sampled from prior.
for
to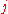 
do % The number of iterations j is chosen by guesswork.
current likelihood values of the points
;
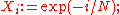
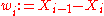
Save the point with least likelihood as a sample point with weight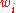
.
Update the point with least likelihood with some Markov Chain
Monte Carlo steps according to the prior, accepting only steps that
keep the likelihood above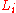
.
end
return
;
At each iteration,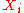
is an estimate of the amount of prior mass covered by
the hypervolume in parameter space of all points with likelihood greater than
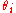. The weight factor
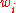is
an estimate of the amount of prior mass that lies between two nested
hypersurfaces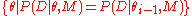
and
. The update step
computes the sum over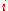
of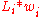 
to numerically approximate the integral
-
The idea is to chop up the range of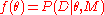
and estimate, for each interval 
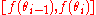, how likely it is a priori that a randomly chosen 
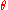would map to this interval. This can be thought of as a Bayesian's way to numerically implement Lebesgue integrationLebesgue integrationIn mathematics, Lebesgue integration, named after French mathematician Henri Lebesgue , refers to both the general theory of integration of a function with respect to a general measure, and to the specific case of integration of a function defined on a subset of the real line or a higher...
.
Simple example code written in CC (programming language)C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
, RR (programming language)R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....
, or PythonPython (programming language)Python is a general-purpose, high-level programming language whose design philosophy emphasizes code readability. Python claims to "[combine] remarkable power with very clear syntax", and its standard library is large and comprehensive...
demonstrating this algorithm can be downloaded from John Skilling's website. There is also a Haskell port on Hackage.
Applications
Since nested sampling was proposed in 2004, it has been used in multiple settings within the field of astronomyAstronomyAstronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
. One paper suggested using nested sampling for cosmologicalCosmologyCosmology is the discipline that deals with the nature of the Universe as a whole. Cosmologists seek to understand the origin, evolution, structure, and ultimate fate of the Universe at large, as well as the natural laws that keep it in order...
model selectionModel selectionModel selection is the task of selecting a statistical model from a set of candidate models, given data. In the simplest cases, a pre-existing set of data is considered...
and object detection, as it "uniquely combines accuracy, general applicability and computational feasibility." A refinement of the nested sampling algorithm to handle multimodal posteriors has also been suggested as a means of detecting astronomical objects in existing datasets.
-
