Neighbourhood components analysis
Encyclopedia
Neighbourhood components analysis is a supervised learning
method for clustering multivariate
data into distinct classes according to a given distance metric
over the data. Functionally, it serves the same purposes as the K-nearest neighbour algorithm, and makes direct use of a related concept termed stochastic nearest neighbours.
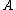corresponding to the transformation can be found by defining a differentiable objective function for 
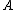, followed by use of an iterative solver such as conjugate gradient descent
. One of the benefits of this algorithm is that the number of classes
can be determined as a function of 
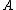, up to a scalar constant. This use of the algorithm therefore addresses the issue of model selection
.
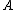, we define an objective function describing classification accuracy in the transformed space and try to determine 
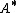such that this objective function is maximized.
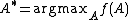
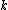-nearest neighbours with a given distance metric. This is known as leave-one-out classification. However, the set of nearest-neighbours 
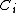can be quite different after passing all the points through a linear transformation. Specifically, the set of neighbours for a point can undergo discrete changes in response to smooth changes in the elements of 
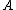, implying that any objective function 
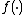based on the neighbours of a point will be piecewise-constant, and hence not differentiable.
. Rather than considering the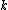
-nearest neighbours at each transformed point in LOO-classification, we'll consider the entire transformed data set as stochastic nearest neighbours. We define these using a softmax function
of the squared Euclidean distance
between a given LOO-classification point and each other point in the transformed space:
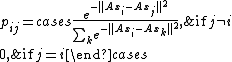
The probability of correctly classifying data point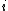
is the probability of classifying the points of each of its neighbours 
:
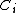where 
is the probability of classifying neighbour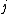 
of point 
.
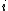Define the objective function using LOO classification, this time using the entire data set as stochastic nearest neighbours:
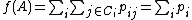
Note that under stochastic nearest neighbours, the consensus class for a single point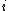
is the expected value of a point's class in the limit of an infinite number of samples drawn from the distribution over its neighbours 
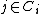i.e.: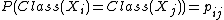 
. Thus the predicted class is an affine combination of the classes of every other point, weighted by the softmax function for each 
where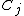 
is now the entire transformed data set.
This choice of objective function is preferable as it is differentiable with respect to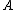
:
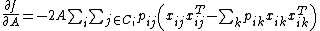
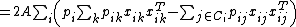
Obtaining a gradient
for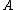
means that it can be found with an iterative solver such as conjugate gradient descent
. Note that in practice, most of the innermost terms of the gradient evaluate to insignificant contributions due to the rapidly diminishing contribution of distant points from the point of interest. This means that the inner sum of the gradient can be truncated, resulting in reasonable computation times even for large data sets.
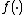is equivalent to minimizing the 
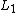-distance between the predicted class distribution and the true class distribution (ie: where the 
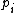induced by 
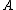are all equal to 1). A natural alternative is the KL-divergence, which induces the following objective function and gradient:" (Goldberger 2005)
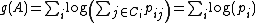
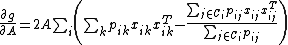
In practice, optimization of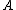
using this function tends to give similar performance results as with the original.
Supervised learning
Supervised learning is the machine learning task of inferring a function from supervised training data. The training data consist of a set of training examples. In supervised learning, each example is a pair consisting of an input object and a desired output value...
method for clustering multivariate
Multivariate statistics
Multivariate statistics is a form of statistics encompassing the simultaneous observation and analysis of more than one statistical variable. The application of multivariate statistics is multivariate analysis...
data into distinct classes according to a given distance metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
over the data. Functionally, it serves the same purposes as the K-nearest neighbour algorithm, and makes direct use of a related concept termed stochastic nearest neighbours.
Definition
Neighbourhood components analysis aims at "learning" a distance metric by finding a linear transformation of input data such that the average leave-one-out (LOO) classification performance is maximized in the transformed space. The key insight to the algorithm is that a matrix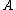 corresponding to the transformation can be found by defining a differentiable objective function for 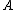, followed by use of an iterative solver such as conjugate gradient descentConjugate gradient method
In mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is symmetric and positive-definite. The conjugate gradient method is an iterative method, so it can be applied to sparse systems that are too...
. One of the benefits of this algorithm is that the number of classes
can be determined as a function of 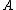, up to a scalar constant. This use of the algorithm therefore addresses the issue of model selectionModel selection
Model selection is the task of selecting a statistical model from a set of candidate models, given data. In the simplest cases, a pre-existing set of data is considered...
.
Explanation
In order to define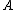, we define an objective function describing classification accuracy in the transformed space and try to determine 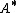such that this objective function is maximized.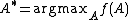Leave-one-out (LOO) classification
Consider predicting the class label of a single data point by consensus of its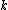-nearest neighbours with a given distance metric. This is known as leave-one-out classification. However, the set of nearest-neighbours 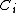can be quite different after passing all the points through a linear transformation. Specifically, the set of neighbours for a point can undergo discrete changes in response to smooth changes in the elements of 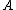, implying that any objective function 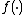based on the neighbours of a point will be piecewise-constant, and hence not differentiable.Solution
We can resolve this difficulty by using an approach inspired by stochastic gradient descentStochastic gradient descent
Stochastic gradient descent is an optimization method for minimizing an objective function that is written as a sum of differentiable functions.- Background :...
. Rather than considering the
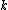-nearest neighbours at each transformed point in LOO-classification, we'll consider the entire transformed data set as stochastic nearest neighbours. We define these using a softmax functionSoftmax activation function
The softmax activation function is a neural transfer function. In neural networks, transfer functions calculate a layer's output from its net input. It is a biologically plausible approximation to the maximum operation...
of the squared Euclidean distance
Euclidean distance
In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
between a given LOO-classification point and each other point in the transformed space:
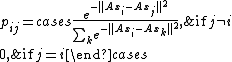
The probability of correctly classifying data point
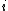is the probability of classifying the points of each of its neighbours 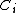: where is the probability of classifying neighbour 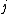of point 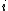.Define the objective function using LOO classification, this time using the entire data set as stochastic nearest neighbours:
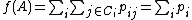
Note that under stochastic nearest neighbours, the consensus class for a single point
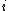is the expected value of a point's class in the limit of an infinite number of samples drawn from the distribution over its neighbours 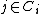i.e.: 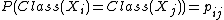. Thus the predicted class is an affine combination of the classes of every other point, weighted by the softmax function for each where 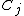is now the entire transformed data set.This choice of objective function is preferable as it is differentiable with respect to
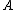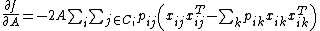
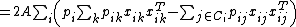
:Obtaining a gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
for
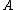means that it can be found with an iterative solver such as conjugate gradient descentConjugate gradient method
In mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is symmetric and positive-definite. The conjugate gradient method is an iterative method, so it can be applied to sparse systems that are too...
. Note that in practice, most of the innermost terms of the gradient evaluate to insignificant contributions due to the rapidly diminishing contribution of distant points from the point of interest. This means that the inner sum of the gradient can be truncated, resulting in reasonable computation times even for large data sets.
Alternative formulation
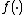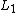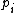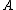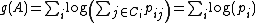
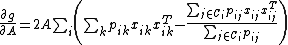
"Maximizing is equivalent to minimizing the -distance between the predicted class distribution and the true class distribution (ie: where the induced by are all equal to 1). A natural alternative is the KL-divergence, which induces the following objective function and gradient:" (Goldberger 2005)In practice, optimization of
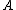using this function tends to give similar performance results as with the original.History and background
Neighbourhood components analysis was developed by Jacob Goldberger, Sam Roweis, Ruslan Salakhudinov, and Geoff Hinton at the University of Toronto's department of computer science in 2004.General
- Neighbourhood Components Analysis (University of Toronto DCS)