Near-field (mathematics)
Encyclopedia
In mathematics
, a near-field is an algebraic structure
similar to a division ring
, except that it has only one of the two distributive laws. Alternatively, a near-field is a near-ring in which there is a multiplicative identity, and every non-zero element has a multiplicative inverse
.
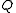, together with two binary operations, ' + ' (addition) and ' • ' (multiplication), satisfying the following axioms:
Zassenhaus proved that all but 7 finite near-fields are either division rings or Dickson near-fields.
The earliest application of the concept of near-field was in the study of geometries, such as projective geometries
. Many projective geometries can be defined in terms of a coordinate system over a division ring, but others can't. It was found that by allowing coordinates from any near-ring the range of geometries which could be coordinatized was extended. For example, the Dickson near-field of order 9 given above allows the construction of a projective plane known as the Hall plane after Marshall Hall
.
There are numerous other applications, mostly to geometry. A more recent application of near-fields is in the construction of ciphers for data-encryption, such as Hill cipher
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a near-field is an algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
similar to a division ring
Division ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
, except that it has only one of the two distributive laws. Alternatively, a near-field is a near-ring in which there is a multiplicative identity, and every non-zero element has a multiplicative inverse
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
.
Definition
A near-field is a set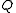, together with two binary operations, ' + ' (addition) and ' • ' (multiplication), satisfying the following axioms:
- A1:
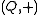is an Abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers... - A2:
• 
• 
= 
• 
• 
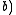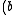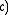for all elements 
, 
, 
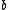of 
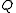(The associative law for multiplication) - A3:
• 
• 
• 
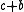for all elements 
, 
, 
of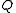 
(The right distributive law) - A4:
contains an element 1 such that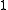 
• 
• 
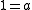for every element 
of 
(Multiplicative identity) - A5: For every non-zero element a of
there exists an element 
−1 such that 
• 
−1 = 1 = 
−1 • 
(Multiplicative inverseMultiplicative inverseIn mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
)
Examples
- Any division ringDivision ringIn abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
(including any fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
) is a near-field. - The following defines a near-field of order 9. It is the smallest near-field which is not a field.
- Let
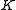be the Galois fieldFinite fieldIn abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
of order 9. Denote multiplication i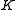n
by ' 
'. Define a new binary operation ' · ' by:
- If
is any element of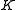 
which is a square and 
is any element of 
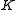then 
· 
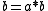
- If
is any element of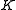 
which is not a square and 
is any element of 
then 
· 
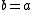3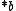
.
- If
- Then
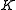is a near-field with this new multiplication and the same addition as before.
- Let
History and Applications
The concept of a near-field was first introduced by L.E. Dickson in 1905. He took division rings and modified their multiplication, while leaving addition as it was, and thus produced the first known examples of near-fields that were not division rings. The near-fields produced by this method are known as Dickson near-fields; the near-field of order 9 given above is a Dickson near-field.Zassenhaus proved that all but 7 finite near-fields are either division rings or Dickson near-fields.
The earliest application of the concept of near-field was in the study of geometries, such as projective geometries
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
. Many projective geometries can be defined in terms of a coordinate system over a division ring, but others can't. It was found that by allowing coordinates from any near-ring the range of geometries which could be coordinatized was extended. For example, the Dickson near-field of order 9 given above allows the construction of a projective plane known as the Hall plane after Marshall Hall
Marshall Hall (mathematician)
Marshall Hall, Jr. was an American mathematician who made contributions to group theory and combinatorics.- Career :...
.
There are numerous other applications, mostly to geometry. A more recent application of near-fields is in the construction of ciphers for data-encryption, such as Hill cipher
Hill cipher
In classical cryptography, the Hill cipher is a polygraphic substitution cipher based on linear algebra. Invented by Lester S. Hill in 1929, it was the first polygraphic cipher in which it was practical to operate on more than three symbols at once. The following discussion assumes an elementary...
s.