
Natural pseudodistance
Encyclopedia
In size theory, the natural pseudodistance between two size pairs 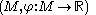 ,
, 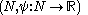 is the value
is the value  , where
, where 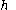 varies in the set of all homeomorphism
varies in the set of all homeomorphism
s from the manifold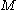 to the manifold
to the manifold 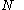 and
and 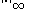 is the supremum norm. If
is the supremum norm. If 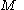 and
and  are not homeomorphic, then the natural pseudodistance is defined to be
are not homeomorphic, then the natural pseudodistance is defined to be 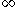 .
.
It is usually assumed that ,
, 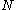 are
are  closed manifold
closed manifold
s and the measuring functions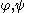 are
are 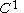 . Put another way, the natural pseudodistance measures the infimum of the change of the measuring function induced by the homeomorphisms from
. Put another way, the natural pseudodistance measures the infimum of the change of the measuring function induced by the homeomorphisms from 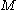 to
to 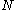 .
.
The concept of natural pseudodistance can be easily extended to size pairs where the measuring function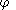 takes values in
takes values in 
.
that the natural pseudodistance always equals the Euclidean distance between two critical values of the measuring functions (possibly, of the same measuring function) divided by a suitable positive integer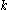 .
.
If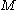 and
and  are surfaces, the number
are surfaces, the number 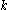 can be assumed to be
can be assumed to be 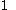 ,
, 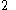 or
or 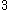 . If
. If 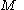 and
and 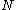 are curves, the number
are curves, the number  can be assumed to be
can be assumed to be 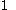 or
or 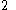 .
.
If an optimal homeomorphism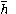 exists (i.e.,
exists (i.e., 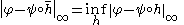 ), then
), then  can be assumed to be
can be assumed to be 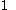 .
.
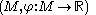 ,
, 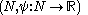 is the value
is the value  , where
, where 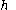 varies in the set of all homeomorphism
varies in the set of all homeomorphismHomeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
s from the manifold
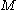 to the manifold
to the manifold 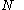 and
and 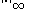 is the supremum norm. If
is the supremum norm. If 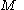 and
and  are not homeomorphic, then the natural pseudodistance is defined to be
are not homeomorphic, then the natural pseudodistance is defined to be 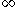 .
.It is usually assumed that
 ,
, 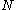 are
are  closed manifold
closed manifoldClosed manifold
In mathematics, a closed manifold is a type of topological space, namely a compact manifold without boundary. In contexts where no boundary is possible, any compact manifold is a closed manifold....
s and the measuring functions
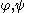 are
are 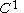 . Put another way, the natural pseudodistance measures the infimum of the change of the measuring function induced by the homeomorphisms from
. Put another way, the natural pseudodistance measures the infimum of the change of the measuring function induced by the homeomorphisms from 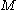 to
to 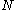 .
.The concept of natural pseudodistance can be easily extended to size pairs where the measuring function
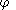 takes values in
takes values in 
.
Main properties
It can be provedthat the natural pseudodistance always equals the Euclidean distance between two critical values of the measuring functions (possibly, of the same measuring function) divided by a suitable positive integer
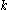 .
.If
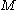 and
and  are surfaces, the number
are surfaces, the number 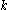 can be assumed to be
can be assumed to be 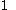 ,
, 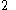 or
or 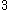 . If
. If 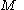 and
and 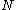 are curves, the number
are curves, the number  can be assumed to be
can be assumed to be 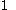 or
or 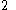 .
.If an optimal homeomorphism
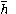 exists (i.e.,
exists (i.e., 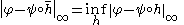 ), then
), then  can be assumed to be
can be assumed to be 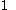 .
.See also
- Fréchet distanceFréchet surfaceIn mathematics, a Fréchet surface is an equivalence class of parametrized surfaces in a metric space. In other words, a Fréchet surface is a way of thinking about surfaces independently of how they are "written down"...
- Size theory
- Size functionSize functionSize functions are shape descriptors, in a geometrical/topological sense. They are functions from the half-plane xSize functions are shape descriptors, in a geometrical/topological sense. They are functions from the half-plane...
- Size functorSize functorGiven a size pair \ where M\ is a manifold of dimensionn\ and f\ is an arbitrary real continuous function definedon it, the i\ -th size functor, with i=0,\ldots,n\ , denoted...
- Size homotopy group
- Size pair

