
Nakagami distribution
Encyclopedia
The Nakagami distribution or the Nakagami-m distribution is a probability distribution
related to the gamma distribution. It has two parameters: a shape parameter
μ and a second parameter controlling spread, ω.
(pdf) is
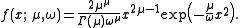
Its cumulative distribution function
is
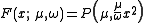
where P is the incomplete gamma function
(regularized).
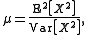
and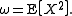
In particular, given a random variable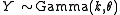 , it is possible to obtain a random variable
, it is possible to obtain a random variable 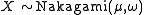 , by setting
, by setting 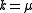 ,
,  , and taking the square root of
, and taking the square root of 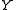 :
:
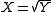 .
.
When 2μ is an integer, the Nakagami distribution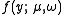 can be generated from the Chi distribution with parameter k set to 2μ and then following it by the scaling transformation:
can be generated from the Chi distribution with parameter k set to 2μ and then following it by the scaling transformation: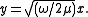
signals traversing multiple paths.
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
related to the gamma distribution. It has two parameters: a shape parameter
Shape parameter
In probability theory and statistics, a shape parameter is a kind of numerical parameter of a parametric family of probability distributions.- Definition :...
μ and a second parameter controlling spread, ω.
Characterization
Its probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
(pdf) is
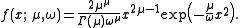
Its cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
is
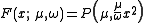
where P is the incomplete gamma function
Incomplete gamma function
In mathematics, the gamma function is defined by a definite integral. The incomplete gamma function is defined as an integral function of the same integrand. There are two varieties of the incomplete gamma function: the upper incomplete gamma function is for the case that the lower limit of...
(regularized).
Parameter estimation
The parameters μ and ω are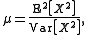
and
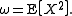
Generation
The Nakagami distribution is related to the gamma distribution.In particular, given a random variable
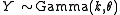 , it is possible to obtain a random variable
, it is possible to obtain a random variable 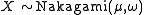 , by setting
, by setting 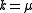 ,
,  , and taking the square root of
, and taking the square root of  :
: .
.When 2μ is an integer, the Nakagami distribution
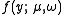 can be generated from the Chi distribution with parameter k set to 2μ and then following it by the scaling transformation:
can be generated from the Chi distribution with parameter k set to 2μ and then following it by the scaling transformation: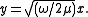
History and applications
The Nakagami distribution is relatively new, being first proposed in 1960. It has been used to model attenuation of wirelessWireless
Wireless telecommunications is the transfer of information between two or more points that are not physically connected. Distances can be short, such as a few meters for television remote control, or as far as thousands or even millions of kilometers for deep-space radio communications...
signals traversing multiple paths.

